Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 11 класс Никольский Параграф 9. Равносильность уравнений и неравенств системам Задание 25
Задание 25
\[\boxed{\mathbf{25.}}\]
\[\textbf{а)}\ \left| f(x) \right| = |g(x)|\]
\[\left\{ \begin{matrix} f(x) = g(x) \\ g(x) \geq 0\ \ \ \ \ \ \\ \end{matrix} \right.\ \ \ и\ \ \left\{ \begin{matrix} f(x) = - g(x) \\ g(x) \geq 0\ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
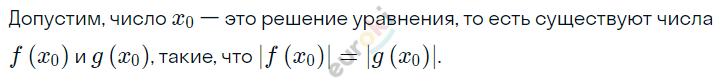
\[По\ определению\ модуля\ имеем\]
\[\ совокупность\ систем:\]
\[\left\{ \begin{matrix} f\left( x_{0} \right) = g\left( x_{0} \right) \\ g\left( x_{0} \right) \geq 0\ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \ \ и\ \]
\[\ \left\{ \begin{matrix} f\left( x_{0} \right) = - g\left( x_{0} \right) \\ g\left( x_{0} \right) \geq 0\ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ .\]
\[Значит,\ x_{0} - это\ решение\]
\[\ совокупности\ систем.\]
\[Следовательно,\ любое\ решение\ \]
\[уравнения\ является\ решением\]
\[совокупности\ систем.\]
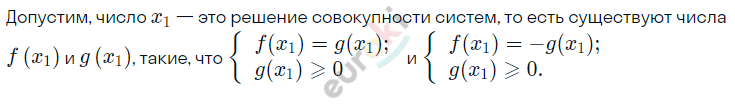
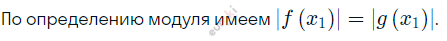
\[Значит,\ x_{1} - это\ решение\ \]
\[уравнения.\]
\[Следовательно,\ любое\ решение\ \]
\[совокупности\ систем\ является\]
\[решением\ уравнения.\]
\[Покажем,\ что\ если\ уравнение\]
\[\ не\ имеет\ решений,\ то\ и\ \]
\[совокупность\]
\[систем\ не\ имеет\ решений.\]
\[Аналогично:если\ совокупность\]
\[\ систем\ не\ имеет\ решения,\]
\[то\ и\ уравнение\ не\ имеет\ \]
\[решения.\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{б)}\ \sqrt{f(x)} + \sqrt{g(x)} =\]
\[= \sqrt{f(x) + g(x)}\]
\[\left\{ \begin{matrix} f(x) = 0 \\ g(x) \geq 0 \\ \end{matrix} \right.\ \text{\ \ \ }и\ \ \ \left\{ \begin{matrix} g(x) = 0 \\ f(x) \geq 0 \\ \end{matrix} \right.\ .\]
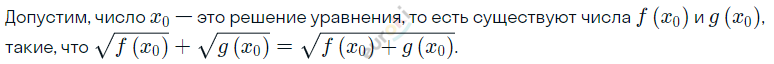
\[Равенство\ возможно,\ когда\]
\[\ одно\ из\ чисел\ равно\ 0:\]
\[\left\{ \begin{matrix} f\left( x_{0} \right) = 0 \\ g\left( x_{0} \right) \geq 0 \\ \end{matrix} \right.\ \text{\ \ \ }и\ \ \ \left\{ \begin{matrix} g\left( x_{0} \right) = 0 \\ f\left( x_{0} \right) \geq 0 \\ \end{matrix} \right.\ .\]
\[Значит,\ x_{0} - это\ решение\ \]
\[совокупности\ систем.\]
\[Следовательно,\ любое\ решение\ \]
\[уравнения\ является\ решением\]
\[совокупности\ систем.\]
\[Значит,\ x_{1} - это\ решение\]
\[\ уравнения.\]
\[Следовательно,\ любое\ решение\]
\[\ совокупности\ систем\ является\]
\[решением\ уравнения.\]
\[Покажем,\ что\ если\ уравнение\ \]
\[не\ имеет\ решений,\ то\ \]
\[и\ совокупность\]
\[систем\ не\ имеет\ решений.\]
\[Аналогично:если\ совокупность\]
\[\ систем\ не\ имеет\ решения,\]
\[то\ и\ уравнение\ не\ имеет\]
\[\ решения.\]
\[Что\ и\ требовалось\ доказать.\]
