Решебник по алгебре 11 класс Никольский Параграф 9. Равносильность уравнений и неравенств системам Задание 23

\[\boxed{\mathbf{23.}}\]

\[\textbf{а)}\ \frac{\sin{2x}}{x} = 0\]

\[\left\{ \begin{matrix} \sin{2x} = 0 \\ x \neq 0\ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x = \frac{\text{πn}}{2} \\ n \neq 0\ \ \ \\ \end{matrix} \right.\ \]

\[Ответ:x = \frac{\text{πn}}{2};n \neq 0.\]

\[\textbf{б)}\ \frac{\sin{2x}}{\sin x} + \frac{\cos{2x}}{\cos x} = 0\ \]

\[\frac{\sin{2x}\cos x + \cos{2x}\sin x}{\sin x\cos x} = 0\]

\[\frac{2\sin{3x}}{\sin{2x}} = 0\]

\[\left\{ \begin{matrix} \sin{3x} = 0 \\ \sin{2x} \neq 0 \\ \end{matrix} \right.\ \]

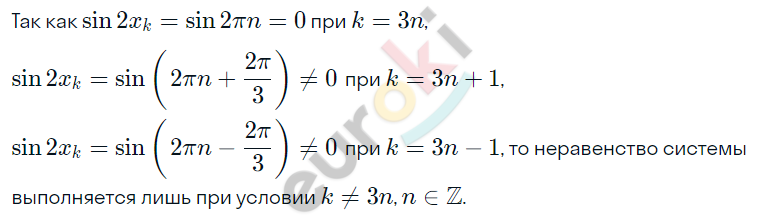
\[Ответ:x = \pm \frac{\pi}{3} + \pi n.\]