Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 778

\[1)\cos^{2}(\alpha + 2\beta) + \sin^{2}(\alpha - 2\beta) - 1 =\]

\[= \cos^{2}(\alpha + 2\beta) - \left( 1 - \sin^{2}(\alpha - 2\beta) \right) =\]

\[= \cos^{2}(\alpha + 2\beta) - \cos^{2}(\alpha - 2\beta) =\]

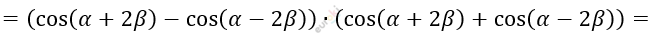
\[= - 2 \bullet \sin\alpha \bullet \sin{2\beta} \bullet 2 \bullet \cos\alpha \bullet \cos{2\beta} =\]

\[= - 2\sin\alpha \bullet \cos\alpha \bullet 2\sin{2\beta} \bullet \cos{2\beta} =\]

\[= - \sin{2\alpha} \bullet \sin{4\beta}.\]

\[2)\sin^{2}(\alpha + 2\beta) + \sin^{2}(\alpha - 2\beta) - 1 =\]

\[= \sin^{2}(\alpha + 2\beta) - \left( 1 - \sin^{2}(\alpha - 2\beta) \right) =\]

\[= \sin^{2}(\alpha + 2\beta) - \cos^{2}(\alpha - 2\beta) =\]

\[= - \cos{2\alpha} \bullet \cos{4\beta}.\]