Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 734

\[\left| \frac{z_{1}}{z_{2}} \right| = \frac{\left| z_{1} \right|}{\left| z_{2} \right|};\text{\ \ \ }z_{2} \neq 0.\]

\[\left| \frac{z_{1}}{z_{2}} \right| = \left| \frac{x_{1} + iy_{1}}{x_{2} + iy_{2}} \right| =\]

\[= \left| \frac{\left( x_{1} + iy_{1} \right)\left( x_{2} - iy_{2} \right)}{\left( x_{2} + iy_{2} \right)\left( x_{2} - iy_{2} \right)} \right| =\]

\[= \left| \frac{x_{1}x_{2} - x_{1}y_{2}i + x_{2}y_{1}i + y_{1}y_{2}}{x_{2}^{2} + y_{2}^{2}} \right| =\]

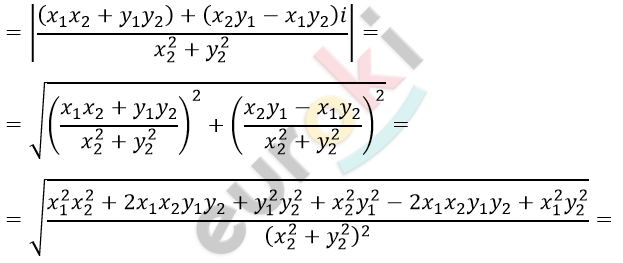
\[= \sqrt{\frac{x_{1}^{2}x_{2}^{2} + x_{1}^{2}y_{2}^{2} + x_{2}^{2}y_{1}^{2} + y_{1}^{2}y_{2}^{2}}{\left( x_{2}^{2} + y_{2}^{2} \right)^{2}}} =\]

\[= \sqrt{\frac{\left( x_{1}^{2} + y_{1}^{2} \right)\left( x_{2}^{2} + y_{2}^{2} \right)}{\left( x_{2}^{2} + y_{2}^{2} \right)^{2}}} =\]

\[= \sqrt{\frac{x_{1}^{2} + y_{1}^{2}}{x_{2}^{2} + y_{2}^{2}}} = \frac{\left| x_{1} + iy_{1} \right|}{\left| x_{2} + iy_{2} \right|} = \frac{\left| z_{1} \right|}{\left| z_{2} \right|}.\]

\[Что\ и\ требовалось\ доказать.\]