Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 642

\[x \neq \pi k;\ \ \ k \in Z.\]

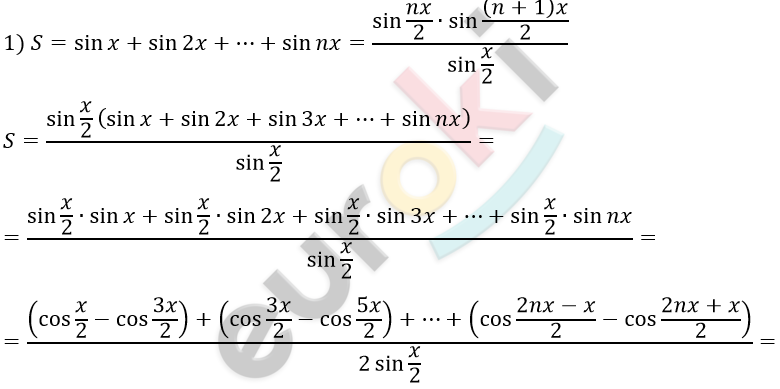
\[= \frac{\cos\frac{x}{2} - \cos\frac{2nx + x}{2}}{2\sin\frac{x}{2}} =\]

\[= \frac{- 2\sin\frac{nx + x}{2} \bullet \sin\frac{- nx}{2}}{2\sin\frac{x}{2}} =\]

\[= \frac{\sin\frac{(n + 1)x}{2} \bullet \sin\frac{\text{nx}}{2}}{\sin\frac{x}{2}}.\]

\[Что\ и\ требовалось\ доказать.\]

\[= 1 + \frac{\sin\frac{2nx + x}{2} - \sin\frac{x}{2}}{2\sin\frac{x}{2}} =\]

\[= \frac{2\sin\frac{x}{2} + \sin\frac{2nx + x}{2} - \sin\frac{x}{2}}{2\sin\frac{x}{2}} =\]

\[= \frac{\sin{\frac{2nx + x}{2} + \sin\frac{x}{2}}}{2\sin\frac{x}{2}} =\]

\[= \frac{2\sin\frac{nx + x}{2} \bullet \cos\frac{\text{nx}}{2}}{2\sin\frac{x}{2}} =\]

\[= \frac{\sin\frac{(n + 1)x}{2} \bullet \cos\frac{\text{nx}}{2}}{\sin\frac{x}{2}}.\]

\[Что\ и\ требовалось\ доказать.\]