Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 608

\[1)\ \frac{5 + 12i}{8 - 6i} + \frac{(1 + 2i)^{2}}{2 + i} =\]

\[= \frac{5 + 12i}{8 - 6i} + \frac{1 + 4i + 4i^{2}}{2 + i} =\]

\[= \frac{- 32 + 126i}{100} + \frac{- 2 + 11i}{5} =\]

\[= \frac{- 32 + 126i}{100} + \frac{- 40 + 220i}{100} =\]

\[= \frac{- 72 + 346i}{100} = - \frac{18}{25} + \frac{173}{50}i.\]

\[2)\ \frac{(1 + 2i)^{2} - (1 - i)^{3}}{(3 + 2i)^{3} - (2 + i)^{2}} =\]

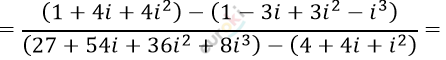
\[= \frac{7i + i^{2} + i^{3}}{23 + 50i + 35i^{2} + 8i^{3}} =\]

\[= \frac{7i - 1 - i}{23 + 50i - 35 - 8i} =\]

\[= \frac{- 1 + 6i}{- 12 + 42i} =\]

\[= \frac{(6i - 1)(42i + 12)}{(42i - 12)(42i + 12)} =\]

\[= \frac{252i^{2} + 72i - 42i - 12}{1764i^{2} - 144} =\]

\[= \frac{- 252 + 30i - 12}{- 1764 - 144} = \frac{- 264 + 30i}{- 1908} =\]

\[= \frac{22}{159} - \frac{5}{318}i.\]

\[Ответ:\ \ \frac{22}{159} - \frac{5}{318}\text{i.}\]