Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 379

\[1)\ y = 9 - x^{2};\ y = 7 - x:\]

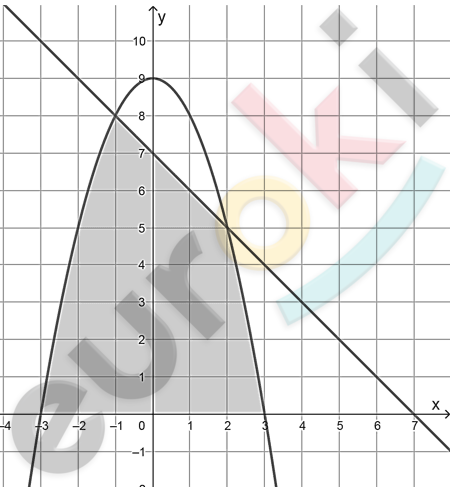
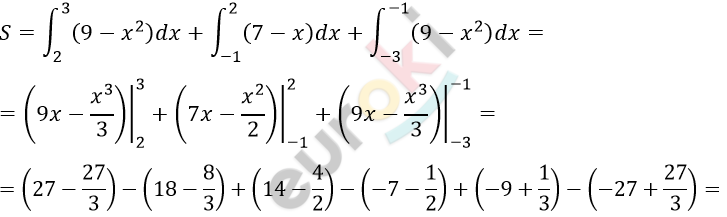
\[= 48 - \frac{45}{3} - \frac{3}{2} = 48 - 15 - 1\frac{1}{2} =\]

\[= 33 - 1\frac{1}{2} = 31\frac{1}{2}.\]

\[Ответ:\ \ 31\frac{1}{2}.\]

\[2)\ y = x(4 - x);\ y = 3:\]

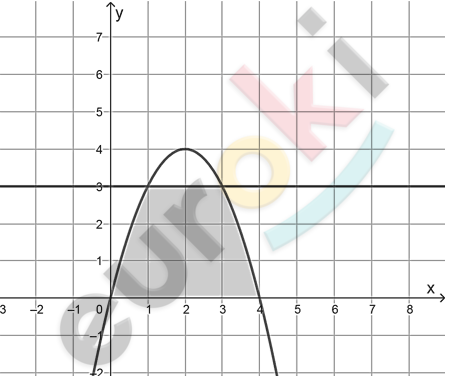
\[y = x(4 - x) = 4x - x^{2}.\]

\[= 32 - 18 + 9 - 3 + 2 - \frac{38}{3} =\]

\[= 22 - 12\frac{2}{3} = 9\frac{1}{3}.\]

\[Ответ:\ \ 9\frac{1}{3}.\]

\[3)\ y = (x - 2)^{2};\ y = (x + 2)^{2};y = 1:\]

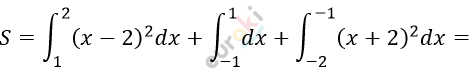
\[= \left. \ \frac{(x - 2)^{3}}{3} \right|_{1}^{2} + \left. \ x \right|_{- 1}^{1} + \left. \ \frac{(x + 2)^{3}}{3} \right|_{- 2}^{- 1} =\]

\[= \frac{0^{3}}{3} - \frac{( - 1)^{3}}{3} + 1 - ( - 1) + \frac{1^{3}}{3} - \frac{0^{3}}{3} =\]

\[= \frac{1}{3} + 1 + 1 + \frac{1}{3} = 2 + \frac{2}{3} = 2\frac{2}{3}.\]

\[Ответ:\ \ 2\frac{2}{3}.\]

\[4)\ y = (x + 2)^{2};\ y = (x - 3)^{2};\]

\[прямая\ ( - 1;\ 1)\ и\ (1;\ 4):\]

\[Уравнение\ прямой:\]

\[1 = k \bullet ( - 1) + b\ \ \]

\[b = k + 1\ \ \ \]

\[2k = 3\]

\[k = \frac{3}{2}.\]

\[4 = k \bullet 1 + b\]

\[4 = k + k + 1\]

\[b = 1 + \frac{3}{2} = \frac{5}{2}.\]

\[= \frac{8}{3} + \frac{10}{2} + \frac{1}{3} = \frac{9}{3} + 5 = 3 + 5 = 8.\]

\[Ответ:\ \ 8.\]

\[5)\ y = \sin x;\ y = \frac{\sqrt{3}}{2};\ \lbrack 0;\ \pi\rbrack:\]

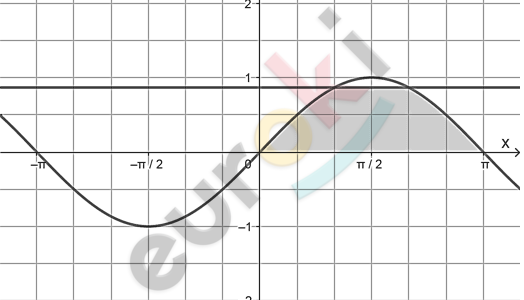
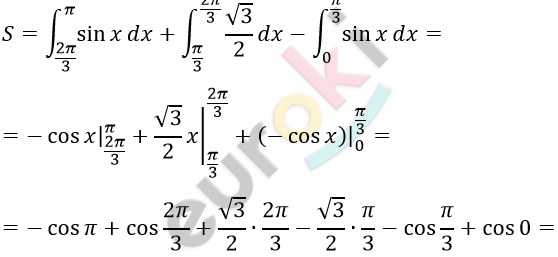
\[= - ( - 1) - \frac{1}{2} + \frac{\sqrt{3}}{2} \bullet \frac{\pi}{3} - \frac{1}{2} + 1 =\]

\[= 2 - 1 + \frac{\pi\sqrt{3}}{6} = \frac{6 + \pi\sqrt{3}}{6}.\]

\[Ответ:\ \ \frac{6 + \pi\sqrt{3}}{6}.\]

\[6)\ y = \cos x;\ y = \frac{1}{2};\ \left\lbrack - \frac{\pi}{2};\ \frac{\pi}{2} \right\rbrack:\]

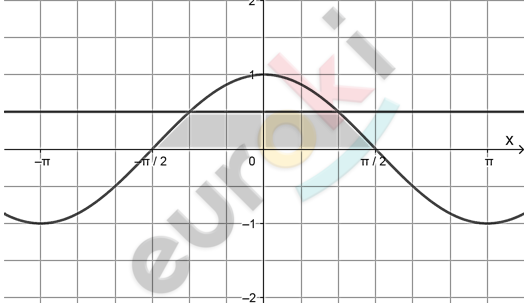
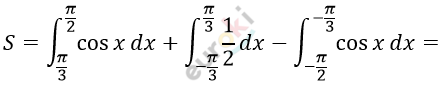
\[= \left. \ \sin x \right|_{\frac{\pi}{3}}^{\frac{\pi}{2}} + \left. \ \frac{1}{2}x \right|_{- \frac{\pi}{3}}^{\frac{\pi}{3}} + \left. \ \sin x \right|_{- \frac{\pi}{2}}^{- \frac{\pi}{3}} =\]

\[= 1 - \frac{\sqrt{3}}{2} + \frac{\pi}{3} - \frac{\sqrt{3}}{2} + 1 =\]

\[= 2 - \sqrt{3} + \frac{\pi}{3}.\]

\[Ответ:\ \ 2 - \sqrt{3} + \frac{\pi}{3}.\]