Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 378

\[1)\ y = \sin x;\ \lbrack 0;\ \pi\rbrack;\]

\[прямая\ (0;\ 0)\ и\ \left( \frac{\pi}{2};\ 1 \right):\]

\[Уравнение\ прямой:\]

\[0 = k \bullet 0 + b\ \ \]

\[b = 0.\ \]

\[1 = k \bullet \frac{\pi}{2} + b\]

\[1 = \frac{\pi}{2}k\]

\[k = \frac{2}{\pi}.\]

\[S = \int_{\frac{\pi}{2}}^{\pi}{\sin x\text{dx}} + \int_{0}^{\frac{\pi}{2}}{\frac{2}{\pi}\text{x\ dx}} =\]

\[= \left. \ - \cos x \right|_{\frac{\pi}{2}}^{\pi} + \left. \ \frac{x^{2}}{\pi} \right|_{0}^{\frac{\pi}{2}} =\]

\[= - \cos\pi + \cos\frac{\pi}{2} + \left( \frac{\pi}{2} \right)^{2}\ :\pi - \frac{0^{2}}{\pi} =\]

\[= 1 + \frac{\pi}{4}.\]

\[Ответ:\ \ 1 + \frac{\pi}{4}.\]

\[2)\ y = \sin x;\ y = \cos x;\ \left\lbrack 0;\ \frac{\pi}{2} \right\rbrack:\]

\[S = \int_{\frac{\pi}{4}}^{\frac{\pi}{2}}{\cos x\text{dx}} + \int_{0}^{\frac{\pi}{4}}{\sin x\text{dx}} =\]

\[= \left. \ \sin x \right|_{\frac{\pi}{4}}^{\frac{\pi}{2}} + \left. \ \left( - \cos x \right) \right|_{0}^{\frac{\pi}{4}} =\]

\[= \sin\frac{\pi}{2} - \sin\frac{\pi}{4} - \cos\frac{\pi}{4} + \cos 0 =\]

\[= 1 - \frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2} + 1 = 2 - \sqrt{2}.\]

\[Ответ:\ \ 2 - \sqrt{2}.\]

\[3)\ y = \sqrt{x};\ \ y = (x - 2)^{2}:\]

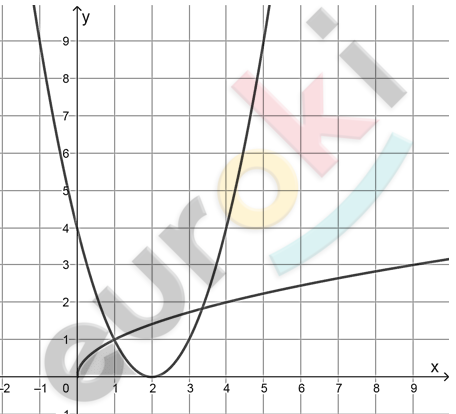
\[S = \int_{1}^{2}{(x - 2)^{2}\text{dx}} + \int_{0}^{1}{\sqrt{x}\text{\ dx}} =\]

\[= \left. \ \frac{(x - 2)^{3}}{3} \right|_{1}^{2} + \left. \ \frac{2}{3}x^{\frac{3}{2}} \right|_{0}^{1} =\]

\[= \frac{(2 - 2)^{3}}{3} - \frac{(1 - 2)^{3}}{3} + \frac{2}{3} \bullet 1^{\frac{3}{2}} - \frac{2}{3} \bullet 0^{\frac{3}{2}}\]

\[= \frac{0^{3}}{3} - \frac{( - 1)^{3}}{3} + \frac{2}{3} - 0 =\]

\[= \frac{1}{3} + \frac{2}{3} = 1.\]

\[Ответ:\ \ 1.\]

\[4)\ y = x^{3};\ y = 2x - x^{2}:\]

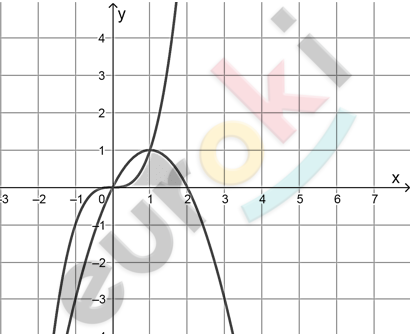
\[S = \int_{1}^{2}{\left( 2x - x^{2} \right)\text{dx}} + \int_{0}^{1}{x^{3}\text{\ dx}} =\]

\[= \left. \ \left( x^{2} - \frac{x^{3}}{3} \right) \right|_{1}^{2} + \left. \ \frac{x^{4}}{4} \right|_{0}^{1} =\]

\[= \left( 2^{2} - \frac{2^{3}}{3} \right) - \left( 1^{2} - \frac{1^{3}}{3} \right) + \frac{1^{4}}{4} - \frac{0^{4}}{4} =\]

\[= \left( 4 - \frac{8}{3} \right) - \left( 1 - \frac{1}{3} \right) + \frac{1}{4} =\]

\[= 3 - \frac{7}{3} + \frac{1}{4} = 3 - \frac{28 - 3}{12} =\]

\[= 3 - \frac{25}{12} = 3 - 2\frac{1}{12} = \frac{11}{12}.\]

\[Ответ:\ \ \frac{11}{12}.\]