Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 351

\[Оба\ автомобиля\ движутся\ к\ \]

\[перекрестку:\]

\[v < 0.\]

\[1)\ S(t) = \sqrt{(a + vt)^{2} + (b + vt)^{2}} =\]

\[= \sqrt{a^{2} + 2avt + v^{2}t^{2} + b^{2} + 2bvt + v^{2}t^{2}} =\]

\[= \sqrt{a^{2} + b^{2} + 2avt + 2bvt + 2v^{2}t^{2}};\]

\[S^{'}(t) =\]

\[= \frac{2av + 2bv + 4v^{2}t}{2\sqrt{a^{2} + b^{2} + 2avt + 2bvt + 2v^{2}t^{2}}}.\]

\[2)\ 2av + 2bv + 4v^{2}t \geq 0\]

\[a + b + 2vt \leq 0\]

\[2vt \leq - (a + b)\]

\[t \geq - \frac{a + b}{2v}.\]

\[3)\ Точка\ минимума:\]

\[t = - \frac{a + b}{2v};\]

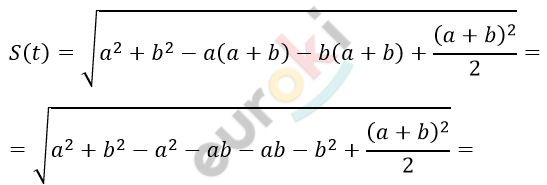
\[= \sqrt{\frac{a^{2} + 2ab + b^{2}}{2} - 2ab} =\]

\[= \sqrt{\frac{a^{2} - 2ab + b^{2}}{2}} =\]

\[= \frac{\sqrt{(a - b)^{2}}}{\sqrt{2}} = \frac{\sqrt{2}}{2}|a - b|.\]

\[Ответ:\ \ \frac{\sqrt{2}}{2}|a - b|.\]