Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 344

\[r - радиус\ основания;\]

\[h - высота\ цилиндра.\]

\[1)\ Радиус\ описанной\ сферы:\]

\[2R = \sqrt{h^{2} + (2r)^{2}}\]

\[4R^{2} = h^{2} + 4r^{2}\]

\[h^{2} = 4R^{2} - 4r^{2}\]

\[h = 2\sqrt{R^{2} - r^{2}}.\]

\[2)\ S(r) = 2\pi r^{2} + 2\pi rh =\]

\[= 2\pi r^{2} + 4\pi r\sqrt{R^{2} - r^{2}};\]

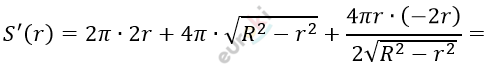
\[= 4\pi r + \frac{4\pi\left( R^{2} - r^{2} \right) - 4\pi r^{2}}{\sqrt{R^{2} - r^{2}}} =\]

\[= \frac{4\pi r\sqrt{R^{2} - r^{2}} + 4\pi R^{2} - 8\pi r^{2}}{\sqrt{R^{2} - r^{2}}}.\]

\[3)\ 4\pi r\sqrt{R^{2} - r^{2}} + 4\pi R^{2} - 8\pi r^{2} \geq 0\]

\[r\sqrt{R^{2} - r^{2}} + R^{2} - 2r^{2} \geq 0\]

\[r\sqrt{R^{2} - r^{2}} \geq 2r^{2} - R^{2}\]

\[r^{2}\left( R^{2} - r^{2} \right) \geq \left( 2r^{2} - R^{2} \right)^{2}\]

\[r^{2}R^{2} - r^{4} \geq 4r^{4} - 4r^{2}R^{2} + R^{4}\]

\[5r^{4} - 5r^{2}R^{2} + R^{4} \leq 0\]

\[D = 25R^{4} - 20R^{4} = 5R^{4}\]

\[r^{2} = \frac{5R^{2} \pm R^{2}\sqrt{5}}{2 \bullet 5} = \frac{R^{2}\left( 5 \pm \sqrt{5} \right)}{10};\]

\[r = \frac{R\sqrt{5 \pm \sqrt{5}}}{\sqrt{10}};\]

\[\frac{R\sqrt{5 - \sqrt{5}}}{\sqrt{10}} \leq r \leq \frac{R\sqrt{5 + \sqrt{5}}}{\sqrt{10}}.\]

\[4)\ Точка\ максимума:\]

\[r = \frac{R\sqrt{5 + \sqrt{5}}}{\sqrt{10}};\]

\[= \frac{\pi R^{2}\left( 5 + \sqrt{5} \right)}{5} + \frac{4\pi R^{2}\sqrt{25 - 5}}{10} =\]

\[= \frac{\pi R^{2}\left( 5 + \sqrt{5} \right)}{5} + \frac{2\pi R^{2} \bullet 2\sqrt{5}}{5} =\]

\[= \frac{\pi R^{2}\left( 5 + 5\sqrt{5} \right)}{5} = \pi R^{2}\left( 1 + \sqrt{5} \right).\]

\[Ответ:\ \ \pi\left( \sqrt{5} + 1 \right)R^{2}.\]