Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 141

\[1)\ f(x) = \frac{x^{2}}{|x|} = |x|;\ \ \ a = 0:\]

\[x \neq 0.\]

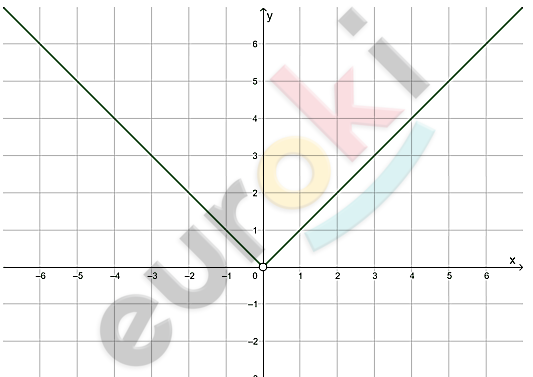
\[Ответ:\ \ 0.\]

\[2)\ f(x) = \frac{x^{2} - 9}{x + 3};\ \ \ a = - 3:\]

\[f(x) = \frac{(x - 3)(x + 3)}{x + 3} = x - 3;\]

\[x + 3 \neq 0\]

\[x \neq - 3.\]

\[Ответ:\ - 6.\]

\[3)\ f(x) = \frac{x^{3} - 1}{x - 1};\ \ a = 1:\]

\[f(x) = \frac{(x - 1)\left( x^{2} + x + 1 \right)}{x - 1} =\]

\[= x^{2} + x + 1;\]

\[x - 1 \neq 0\]

\[x \neq 1.\]

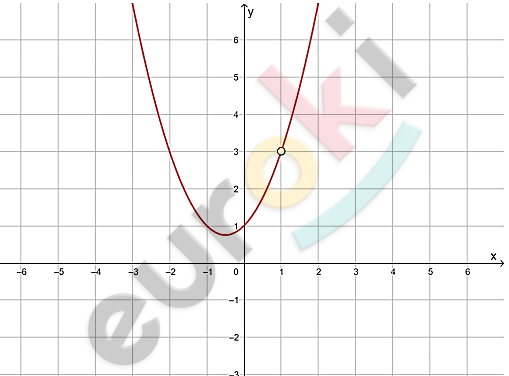
\[Ответ:\ \ 3.\]

\[4)\ f(x) = \frac{2x^{2} - x - 6}{x - 2};\ \ \ a = 2:\]

\[f(x) = \frac{(2x + 3)(x - 2)}{x - 2} = 2x + 3;\]

\[x - 2 \neq 0\]

\[x \neq 2.\]

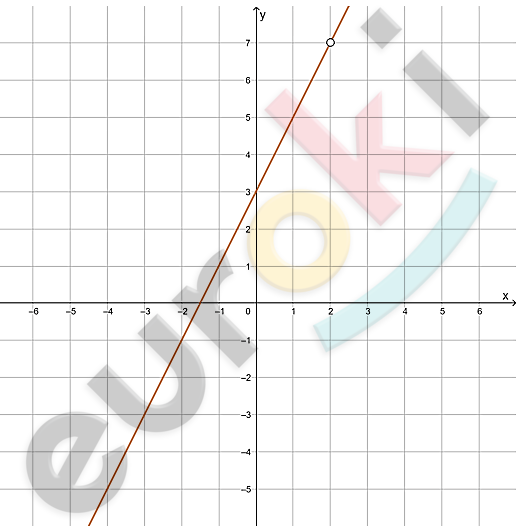
\[Ответ:\ \ 7.\]