Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 138

\[1)\ x_{n} = \frac{5n + 2}{3n + 4}:\]

\[\lim_{x \rightarrow \infty}\frac{5n + 2}{3n + 4} = \lim_{x \rightarrow \infty}\frac{5 + \frac{2}{n}}{3 + \frac{4}{n}} =\]

\[= \frac{5 + 0}{3 + 0} = \frac{5}{3}.\]

\[2)\ x_{n} = \frac{n^{2} - n + 2}{3n^{2} + 7}:\]

\[\lim_{x \rightarrow \infty}\frac{n^{2} - n + 2}{3n^{2} + 7} = \lim_{x \rightarrow \infty}\frac{1 - \frac{1}{n} + \frac{2}{n^{2}}}{3 + \frac{7}{n^{2}}} =\]

\[= \frac{1 - 0 + 0}{3 + 0} = \frac{1}{3}.\]

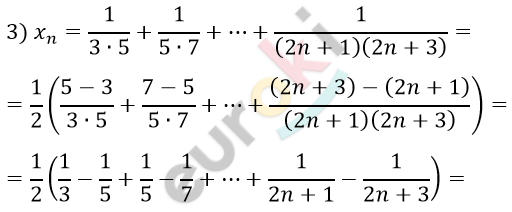
\[= \frac{1}{2}\left( \frac{1}{3} - \frac{1}{2n + 3} \right) =\]

\[= \frac{1}{2} \bullet \frac{2n + 3 - 3}{3(2n + 3)} = \frac{n}{6n + 9}:\]

\[\lim_{x \rightarrow \infty}\frac{n}{6n + 9} = \lim_{x \rightarrow \infty}\frac{1}{6 + \frac{9}{n}} =\]

\[= \frac{1}{6 + 0} = \frac{1}{6}.\]

\[4)\ x_{n} = \frac{1 + 2 + \ldots + n}{n^{2}} =\]

\[= \frac{1 + n}{2} \bullet n \bullet \frac{1}{n^{2}\ } = \frac{1 + n}{2n}:\]

\[\lim_{x \rightarrow \infty}\frac{1 + n}{2n} = \lim_{x \rightarrow \infty}\frac{\frac{1}{n} + 1}{2} =\]

\[= \frac{0 + 1}{2} = \frac{1}{2}.\]

\[5)\ x_{n} = \sqrt{\frac{3n + 5}{2n - 1}}:\]

\[\lim_{x \rightarrow \infty}\sqrt{\frac{3n + 5}{2n - 1}} = \lim_{x \rightarrow \infty}\sqrt{\frac{3 + \frac{5}{n}}{2 - \frac{1}{n}}} =\]

\[= \sqrt{\frac{3 + 0}{2 - 0}} = \sqrt{\frac{3}{2}}.\]

\[6)\ x_{n} = \sqrt{n^{2} - n + 2} - n =\]

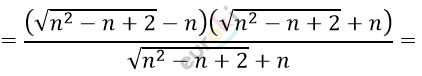
\[= \frac{n^{2} - n + 2 - n^{2}}{\sqrt{n^{2} - n + 2} + n} =\]

\[= \frac{2 - n}{\sqrt{n^{2} - n + 2} + n}:\]

\[\lim_{x \rightarrow \infty}\frac{2 - n}{\sqrt{n^{2} - n + 2} + n} =\]

\[= \lim_{x \rightarrow \infty}\frac{\frac{2}{n} - 1}{\sqrt{1 - \frac{1}{n} + \frac{2}{n^{2}}} + 1} = - \frac{1}{2}.\]