Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 1101

\[y = 9x - x^{3};\text{\ \ \ }x_{0} = 3:\]

\[y^{'}(x) = (9x)^{'} - \left( x^{3} \right)^{'} = 9 - 3x^{2};\]

\[y^{'}(3) = 9 - 3 \bullet 9 = 9 - 27 = - 18;\]

\[y(3) = 9 \bullet 3 - 3^{3} = 27 - 27 = 0;\]

\[y = 0 - 18(x - 3) = 54 - 18x.\]

\[\ Точки\ пересечения:\]

\[9x - x^{3} = 54 - 18x\]

\[x^{3} - 27x + 54 = 0\]

\[(x - 3)\left( x^{2} + 3x - 18 \right) = 0\]

\[D = 9 + 72 = 81\]

\[x_{1} = \frac{- 3 - 9}{2} = - 6;\]

\[x_{2} = \frac{- 3 + 9}{2} = 3.\]

\[S = \int_{- 6}^{3}{\left( 9x - x^{3} - 54 + 18x \right)\text{dx}} =\]

\[= \int_{- 6}^{3}{\left( 27x - x^{3} - 54 \right)\text{dx}} =\]

\[= \left. \ \left( \frac{27x^{2}}{2} - \frac{x^{4}}{4} - 54x \right) \right|_{- 6}^{3} =\]

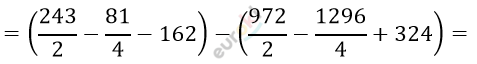
\[= - \frac{729}{2} + \frac{1215}{4} - 486 =\]

\[= - 364,5 + 303,75 - 486 =\]

\[= - 546,75.\]

\[Ответ:\ \ 546,75.\]