Решебник по алгебре и начала математического анализа 11 класс Колягин Проверь себя I. Сложный вариант

\[\mathbf{1}\text{.\ }\]

\[y = - \cos x:\]

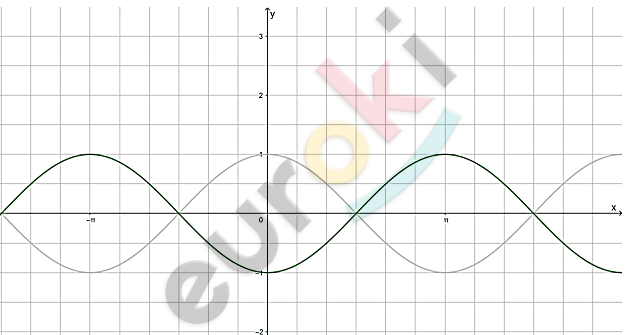
\[\textbf{а)}\ - \frac{\pi}{2} + 2\pi n < x < \frac{\pi}{2} + 2\pi n;\]

\[\textbf{б)}\ - \pi + 2\pi n \leq x \leq 2\pi n.\]

\[\mathbf{2.}\ \]

\[y = \sin\left( \frac{\pi}{3} - x \right):\]

\[- \frac{2\pi}{3} + 2\pi n < x < \frac{\pi}{3} + 2\pi n.\]

\[\mathbf{3.}\]

\[\cos x = \lg x;\]

\[\mathbf{\ }y = \cos x\ и\ y = \lg x:\]

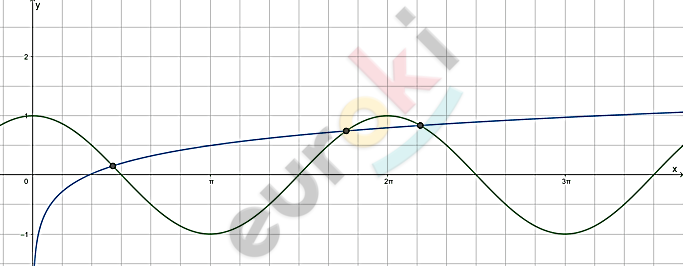
\[\mathbf{О}твет:\ \ 3\ решения.\]

\[\mathbf{4}\text{.\ }\]

\[y = \sin^{2}x + 2\cos{2x}\]

\[y = \sin^{2}x + 2\left( 1 - 2\sin^{2}x \right)\]

\[y = 2 - 3\sin^{2}x.\]

\[0 \leq \sin^{2}x \leq 1\]

\[- 3 \leq - 3\sin^{2}x \leq 0\]

\[- 1 \leq 2 - 3\sin^{2}x \leq 2.\]

\[Ответ:\ \ E(y) = \lbrack - 1;\ 2\rbrack.\]

\[\mathbf{5.\ }\]

\[y = \frac{1}{2}\sin\left( 2x - \frac{\pi}{3} \right) + 1\]

\[D(x) = ( - \infty;\ + \infty);\]

\[- 1 \leq \sin\varphi \leq 1\]

\[- \frac{1}{2} \leq \frac{1}{2}\sin\varphi \leq \frac{1}{2}\]

\[\frac{1}{2} \leq \frac{1}{2}\sin\varphi + 1 \leq \frac{3}{2}\]

\[E(y) = \left\lbrack \frac{1}{2};\ \frac{3}{2} \right\rbrack.\]

\[Промежуток\ возрастания:\]

\[y^{'}(x) = \frac{1}{2} \bullet 2\cos\left( 2x - \frac{\pi}{3} \right) \geq 0\]

\[\cos\left( 2x - \frac{\pi}{3} \right) \geq 0\]

\[- \frac{\pi}{2} + 2\pi n \leq 2x - \frac{\pi}{3} \leq \frac{\pi}{2} + 2\pi n\]

\[- \frac{\pi}{6} + 2\pi n \leq 2x \leq \frac{5\pi}{6} + 2\pi n\]

\[- \frac{\pi}{12} + \pi n \leq x \leq \frac{5\pi}{12} + \pi n.\]