Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 966

\[\boxed{\mathbf{966}\mathbf{.}}\]

\[y = 1,8x^{5} - 2\frac{1}{3}x^{3} + 7x + 12,5\]

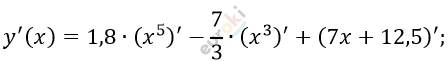
\[y^{'}(x) = 1,8 \bullet 5x^{4} - \frac{7}{3} \bullet 3x^{2} + 7 =\]

\[= 9x^{4} - 7x^{2} + 7.\]

\[Стационарные\ точки:\]

\[9x^{4} - 7x^{2} + 7 = 0\]

\[D = 7^{2} - 4 \bullet 9 \bullet 7 = 49 - 252 =\]

\[= - 203\]

\[D < 0 \rightarrow корней\ нет.\]

\[y^{'}(0) = 9 \bullet 0^{4} - 7 \bullet 0^{2} + 7 =\]

\[= 7 > 0.\]

\[Функция\ возрастает\ на\ всей\ \]

\[области\ определения.\ \]

\[Что\ и\ требовалось\ доказать.\]