Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 961
Задание 961
\[\boxed{\mathbf{961}\mathbf{.}}\]
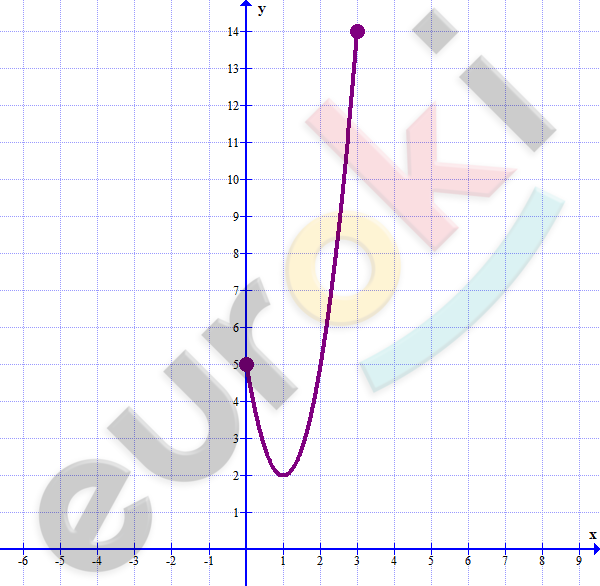
\[1)\ y = 3x^{2} - 6x + 5;\ \ \ \lbrack 0;\ 3\rbrack\]
\[\textbf{а)}\ D(x) = ( - \infty;\ + \infty);\]
\[\textbf{б)}\ y^{'}(x) =\]
\[= 3 \bullet \left( x^{2} \right)^{'} - (6x - 5)^{'} =\]
\[= 3 \bullet 2x - 6 = 6x - 6;\]
\[\textbf{в)}\ Стационарные\ точки:\]
\[6x - 6 = 0\]
\[x - 1 = 0\ \]
\[x = 1.\]
\[\textbf{г)}\ f(0) = 3 \bullet 0^{2} - 6 \bullet 0 + 5 = 5;\]
\[f(1) = 3 \bullet 1^{2} - 6 \bullet 1 + 5 =\]
\[= 3 - 6 + 5 = 2;\]
\[f(3) = 3 \bullet 3^{2} - 6 \bullet 3 + 5 =\]
\[= 27 - 18 + 5 = 14.\]
\[\textbf{д)}\ Возрастает\ на\ (1;\ 3)\ и\ \]
\[убывает\ на\ (0;\ 1);\]
\[x = 1 - точка\ минимума.\]
\[\textbf{е)}\ \]
| \[x\] | \[0\] | \[0 < x < 1\] | \[1\] | \[1 < x < 3\] | \[3\] |
|---|---|---|---|---|---|
| \[f^{'}(x)\] | \[-\] | \[-\] | \[0\] | \[+\] | \[+\] |
| \[f(x)\] | \[5\] | \[\searrow\] | \[2\] | \[\nearrow\] | \[14\] |
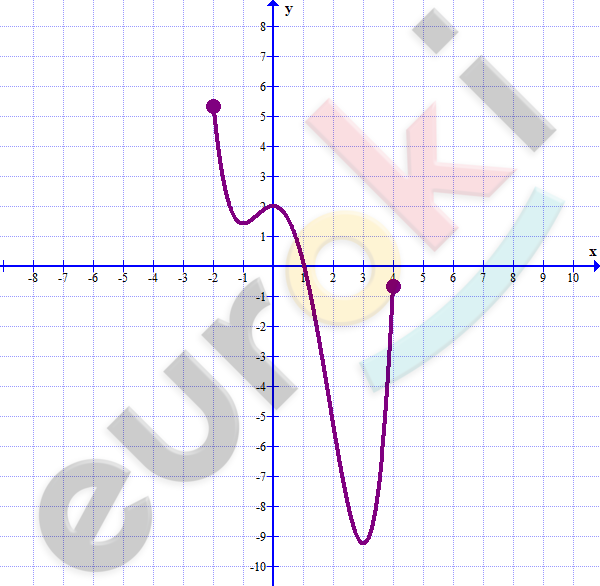
\[2)\ y = \frac{1}{4}x^{4} - \frac{2}{3}x^{3} - \frac{3}{2}x^{2} + 2;\ \ \ \]
\[\lbrack - 2;\ 4\rbrack;\]
\[\textbf{а)}\ D(x) = ( - \infty;\ + \infty);\]
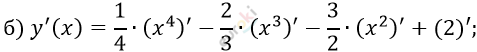
\[y^{'}(x) =\]
\[= \frac{1}{4} \bullet 4x^{3} - \frac{2}{3} \bullet 3x^{2} - \frac{3}{2} \bullet 2x + 0 =\]
\[= x^{3} - 2x^{2} - 3x.\]
\[\textbf{в)}\ Стационарные\ точки:\]
\[x^{3} - 2x^{2} - 3x = 0\]
\[x \bullet \left( x^{2} - 2x - 3 \right) = 0\]
\[D = 2^{2} + 4 \bullet 3 = 4 + 12 = 16\]
\[x_{1} = \frac{2 - 4}{2} = - 1\ \ и\ \ \]
\[x_{2} = \frac{2 + 4}{2} = 3.\]
\[(x + 1) \bullet x \bullet (x - 3) = 0\]
\[x_{1} = - 1,\ \ \ x_{2} = 0,\ \ \ x_{3} = 3.\]
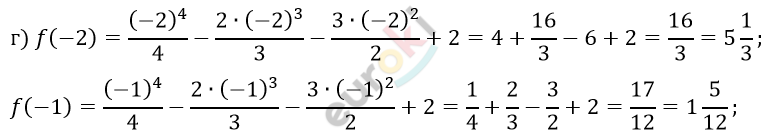
\[f(0) =\]
\[= \frac{0^{4}}{4} - \frac{2 \bullet 0^{3}}{3} - \frac{3 \bullet 0^{2}}{2} + 2 = 2;\]
\[f(3) = \frac{3^{4}}{4} - \frac{2 \bullet 3^{3}}{3} - \frac{3 \bullet 3^{2}}{2} + 2 =\]
\[= \frac{81}{4} - 18 - \frac{27}{2} + 2 = - \frac{37}{4} =\]
\[= - 9\frac{1}{4};\]
\[f(4) = \frac{4^{4}}{4} - \frac{2 \bullet 4^{3}}{3} - \frac{3 \bullet 4^{2}}{2} + 2 =\]
\[= 64 - \frac{128}{3} - 24 + 2 = - \frac{2}{3}.\]
\[\textbf{д)}\ Возрастает\ \]
\[на\ ( - 1;\ 0) \cup (3;\ 4)\ и\ убывает\ \]
\[на\ ( - 2;\ - 1) \cup (0;\ 3);\]
\[x = - 1\ и\ x = 3 - точки\ \]
\[минимума;\ \ \]
\[x = 0 - точка\ максимума.\]
\[\textbf{е)}\ Таблица\ свойств\ функции:\]
| \[x\] | \[- 2\] | \[- 2 < x < - 1\] | \[- 1\] | \[- 1 < x < 0\] | \[0\] | \[0 < x < 3\] | \[3\] | \[3 < x < 4\] | \[4\] |
|---|---|---|---|---|---|---|---|---|---|
| \[f^{'}(x)\] | \[-\] | \[-\] | \[0\] | \[+\] | \[0\] | \[-\] | \[0\] | \[+\] | \[+\] |
| \[f(x)\] | \[5\frac{1}{3}\] | \[\searrow\] | \[1\frac{5}{12}\] | \[\nearrow\] | \[2\] | \[\searrow\] | \[- 9\frac{1}{4}\] | \[\nearrow\] | \[- \frac{2}{3}\] |