Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 949

\[\boxed{\mathbf{949}\mathbf{.}}\]

\(\mathbf{Пусть\ }KD = a:\)

\[BD = BK + KD = x + a.\]

\[Рассмотрим\ параллельные\ \]

\[прямые\ \text{MN\ }и\ \text{AC\ }и\ \]

\[секущую\ AB:\]

\[\angle BMN = \angle BAC\ \]

\[(как\ соответственные\ углы)\text{.\ }\]

\[Треугольники\ \text{ABC\ }и\ \text{BMN\ }\]

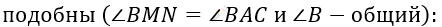
\[\frac{\text{AC}}{\text{MN}} = \frac{\text{BD}}{\text{BK}} = \frac{x + a}{x};\]

\[AC = \frac{(x + a) \bullet MN}{x} =\]

\[= \frac{(x + a) \bullet a}{x} = \frac{ax + a^{2}}{x} =\]

\[= a + \frac{a^{2}}{x}.\]

\[Площадь\ треугольника:\]

\[S(x) = \frac{1}{2} \bullet AC \bullet BD =\]

\[= \frac{1}{2} \bullet \left( a + \frac{a^{2}}{x} \right) \bullet (x + a);\]

\[S(x) =\]

\[= \frac{1}{2} \bullet \left( ax + a^{2} + a^{2} + \frac{a^{3}}{x} \right) =\]

\[= \frac{1}{2} \bullet \left( 2a^{2} + ax + \frac{a^{3}}{x} \right) =\]

\[= a^{2} + \frac{\text{ax}}{2} + \frac{a^{3}}{2x}.\]

\[Производная\ функции:\]

\[S^{'}(x) =\]

\[= \left( a^{2} \right)^{'} + \frac{a}{2} \bullet (x)^{'} + \frac{a^{3}}{2} \bullet \left( \frac{1}{x} \right)^{'};\]

\[S^{'}(x) = 0 + \frac{a}{2} - \frac{a^{3}}{2x^{2}} =\]

\[= \frac{a}{2} \bullet \left( 1 - \frac{a^{2}}{x^{2}} \right).\]

\[Промежуток\ возрастания:\]

\[1 - \frac{a^{2}}{x^{2}} > 0\]

\[x^{2} - a^{2} > 0\]

\[x^{2} > a^{2}\]

\[x < - a\ или\ x > a.\]

\[x = a - точка\ минимума.\]

\[Ответ:\ \ \text{BK} = a.\ \]