Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 948

\[\boxed{\mathbf{948}\mathbf{.}}\]

\[Высота\ коробки\ равна\ стороне\ \]

\[отрезаемого\ квадрата:\]

\[V(x) = S_{осн} \bullet h.\]

\[V(x) = (a - 2x)^{2} \bullet x =\]

\[= \left( a^{2} - 4ax + 4x^{2} \right) \bullet x =\]

\[= a^{2} \bullet x - 4ax^{2} + 4x^{3} =\]

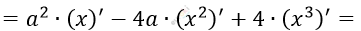
\[= a^{2} - 4a \bullet 2x + 4 \bullet 3x^{2} =\]

\[= 12x^{2} - 8ax + a^{2}.\]

\[Промежуток\ возрастания:\]

\[12x^{2} - 8ax + a^{2} = 0\]

\[D = (8a)^{2} - 4 \bullet 12 \bullet a^{2} =\]

\[= 64a^{2} - 48a^{2} = 16a^{2}\]

\[x_{1} = \frac{8a - 4a}{2 \bullet 12} = \frac{4a}{24} = \frac{a}{6};\ \ \]

\[x_{2} = \frac{8a + 4a}{2 \bullet 12} = \frac{12a}{24} = \frac{a}{2}.\]

\[\left( x - \frac{a}{6} \right)\left( x - \frac{a}{2} \right) > 0\]

\[x < \frac{a}{6}\ или\ x > \frac{a}{2}.\]

\[x = \frac{a}{6} - точка\ максимума.\]

\[Ответ:\ \ \frac{a}{6}.\]