Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 915

\[\boxed{\mathbf{915}\mathbf{.}}\]

\[1)\ y = x^{3} - 3x^{2}\]

\[y^{'}(x) = \left( x^{3} \right)^{'} - 3 \bullet \left( x^{2} \right)^{'} =\]

\[= 3x^{2} - 3 \bullet 2x = 3x^{2} - 6x.\]

\[Точки\ экстремума:\]

\(3x^{2} - 6x = 0\)

\[3x \bullet (x - 2) = 0.\]

\[y(0) = 0^{3} - 3 \bullet 0^{2} = 0;\]

\[y(2) = 2^{3} - 3 \bullet 2^{2} = 8 - 3 \bullet 4 =\]

\[= 8 - 12 = - 4.\]

\[Ответ:\ \ x = 2 - точка\ \]

\[минимума,\ \ \ y(2) = - 4;\]

\[x = 0 - точка\ максимума,\ \ \ \]

\[y(0) = 0.\]

\[2)\ y = x^{4} - 8x^{2} + 3\]

\[y^{'}(x) = \left( x^{4} \right)^{'} - 8 \bullet \left( x^{2} \right)^{'} + (3)^{'} =\]

\[= 4x^{3} - 8 \bullet 2x + 0 = 4x^{3} - 16x.\]

\[Точки\ экстремума:\]

\[4x^{3} - 16x = 0\]

\[4x \bullet \left( x^{2} - 4 \right) = 0\]

\[(x + 2) \bullet 4x \bullet (x - 2) = 0.\]

\[y( \pm 2) = ( \pm 2)^{4} - 8 \bullet ( \pm 2)^{2} + 3 =\]

\[= 16 - 8 \bullet 4 + 3 = 19 - 32 =\]

\[= - 13;\]

\[y(0) = 0^{4} - 8 \bullet 0^{2} + 3 = 3.\]

\[Ответ:\ \ x = \pm 2 - точки\ \]

\[минимума,\ \ \ f( \pm 2) = - 13;\]

\[x = 0 - точка\ максимума,\ \ \ \]

\[f(0) = 3.\]

\[3)\ y = x + \sin x\]

\[y^{'}(x) = (x)^{'} + \left( \sin x \right)^{'} =\]

\[= 1 + \cos x.\]

\[Точки\ экстремума:\]

\[- 1 \leq \cos x \leq 1\]

\[0 \leq 1 + \cos x \leq 1.\]

\[Ответ:\ \ нет\ таких\ точек.\]

\[4)\ y = 2\cos x + x\]

\[y^{'}(x) = 2 \bullet \left( \cos x \right)^{'} + (x)^{'} =\]

\[= - 2\sin x + 1.\]

\[Промежуток\ убывания:\]

\[- 2\sin x + 1 < 0\]

\[- 2\sin x < - 1\]

\[\sin x > \frac{1}{2}.\]

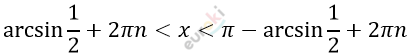
\[\frac{\pi}{6} + 2\pi n < x < \pi - \frac{\pi}{6} + 2\pi n\]

\[\frac{\pi}{6} + 2\pi n < x < \frac{5\pi}{6} + 2\pi n.\]

\[y\left( \frac{\pi}{6} + 2\pi n \right) =\]

\[= 2\cos\left( \frac{\pi}{6} \right) + \frac{\pi}{6} + 2\pi n =\]

\[= \sqrt{3} + \frac{\pi}{6} + 2\pi n;\]

\[y\left( \frac{5\pi}{6} + 2\pi n \right) =\]

\[= 2\cos\left( \frac{5\pi}{6} \right) + \frac{5\pi}{6} + 2\pi n =\]

\[= - \sqrt{3} + \frac{5\pi}{6} + 2\pi n.\]

\[Ответ:\ \ x = \frac{5\pi}{6} + 2\pi n - точка\ \]

\[минимума,\ \ \ y\left( \frac{5\pi}{6} + 2\pi n \right) =\]

\[= - \sqrt{3} + \frac{5\pi}{6} + 2\pi n;\]

\[x = \frac{\pi}{6} + 2\pi n - точка\ \]

\[максимума,\ \ \ \]

\[y\left( \frac{\pi}{6} + 2\pi n \right) = \sqrt{3} + \frac{\pi}{6} + 2\pi n.\]