Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 900

\[\boxed{\mathbf{900}\mathbf{.}}\]

\[1)\ y = x^{2} - x\]

\[y^{'}(x) = \left( x^{2} \right)^{'} - (x)^{'} = 2x - 1.\]

\[Промежуток\ возрастания:\]

\[2x - 1 > 0\]

\[2x > 1\]

\[\ x > 0,5.\]

\[Ответ:\ \ возрастает\ на\ (0,5;\ + \infty)\ \]

\[и\ убывает\ на\ ( - \infty;\ 0,5).\]

\[2)\ y = 5x^{2} - 3x - 1\]

\[y^{'}(x) = 5\left( x^{2} \right)^{'} - (3x + 1)^{'} =\]

\[= 5 \bullet 2x - 3 = 10x - 3.\]

\[Промежуток\ возрастания:\]

\[10x - 3 > 0\]

\[10x > 3\ \]

\[x > 0,3.\]

\[Ответ:\ \ возрастает\ на\ (0,3;\ + \infty)\ \]

\[и\ убывает\ на\ ( - \infty;\ 0,3).\]

\[3)\ y = x^{2} + 2x\]

\[y^{'}(x) = \left( x^{2} \right)^{'} + (2x)^{'} = 2x + 2 =\]

\[= 2(x + 1).\]

\[Промежуток\ возрастания:\]

\[x + 1 > 0\ \]

\[x > - 1.\]

\[Ответ:\ \ возрастает\ на\ ( - 1;\ + \infty)\ \]

\[и\ убывает\ на\ ( - \infty;\ - 1).\]

\[4)\ y = x^{2} + 12x - 100\]

\[y^{'}(x) = \left( x^{2} \right)^{'} + (12x - 100)^{'} =\]

\[= 2x + 12 = 2(x + 6).\]

\[Промежуток\ возрастания:\]

\[x + 6 > 0\ \]

\[x > - 6.\]

\[Ответ:\ \ возрастает\ на\ ( - 6;\ + \infty)\ \]

\[и\ убывает\ на\ ( - \infty;\ - 6).\]

\[5)\ y = x^{3} - 3x\]

\[y^{'}(x) = \left( x^{3} \right)^{'} - (3x)^{'} =\]

\[= 3x^{2} - 3 = 3\left( x^{2} - 1 \right).\]

\[Промежуток\ возрастания:\]

\[x^{2} - 1 > 0\]

\[x^{2} > 1\]

\[x < - 1\ или\ x > 1.\]

\[Ответ:\ \ возрастает\ на\ \]

\[( - \infty;\ - 1) \cup (1;\ + \infty)\ и\ убывает\ \]

\[на\ ( - 1;\ 1).\]

\[6)\ y = x^{4} - 2x^{2}\]

\[y^{'}(x) = \left( x^{4} \right)^{'} - 2\left( x^{2} \right)^{'} =\]

\[= 4x^{3} - 2 \bullet 2x = 4x^{3} - 4x.\]

\[Промежуток\ возрастания:\]

\[4x^{3} - 4x > 0\]

\[4x\left( x^{2} - 1 \right) > 0\]

\[(x + 1) \bullet 4x \bullet (x - 1) > 0\]

\[- 1 < x < 0\ или\ x > 1.\]

\[Ответ:\ \ возрастает\ \]

\[на\ ( - 1;\ 0) \cup (1;\ + \infty)\ и\ убывает\ \]

\[на\ ( - \infty;\ - 1) \cup (0;\ 1).\]

\[7)\ y = 2x^{3} - 3x^{2} - 36x + 40\]

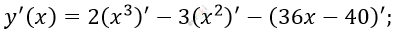
\[y^{'}(x) = 2 \bullet 3x^{2} - 3 \bullet 2x - 36 =\]

\[= 6x^{2} - 6x - 36.\]

\[Промежуток\ возрастания:\]

\[6x^{2} - 6x - 36 > 0\]

\[x^{2} - x - 6 > 0\]

\[D = 1^{2} + 4 \bullet 6 = 1 + 24 = 25\]

\[x_{1} = \frac{1 - 5}{2} = - 2;\text{\ \ }\]

\[x_{2} = \frac{1 + 5}{2} = 3.\]

\[(x + 2)(x - 3) > 0.\]

\[x < - 2\ или\ x > 3.\]

\[Ответ:\ \ возрастает\ \]

\[на\ ( - \infty;\ - 2) \cup (3;\ + \infty)\ и\ \]

\[убывает\ на\ ( - 2;\ 3).\]

\[8)\ y = x^{3} - 6x^{2} + 9\]

\[y^{'}(x) = \left( x^{3} \right)^{'} - 6\left( x^{2} \right)^{'} + (9)^{'};\]

\[y^{'}(x) = 3x^{2} - 6 \bullet 2x + 0 =\]

\[= 3x^{2} - 12x.\]

\[Промежуток\ возрастания:\]

\[3x^{2} - 12x > 0\]

\[3x \bullet (x - 4) > 0\]

\[x < 0\ или\ x > 4.\]

\[Ответ:\ \ возрастает\ \]

\[на\ ( - \infty;\ 0) \cup (4;\ + \infty)\ и\ \]

\[убывает\ на\ (0;\ 4).\]