Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 719

\[\boxed{\mathbf{719}\mathbf{.}}\]

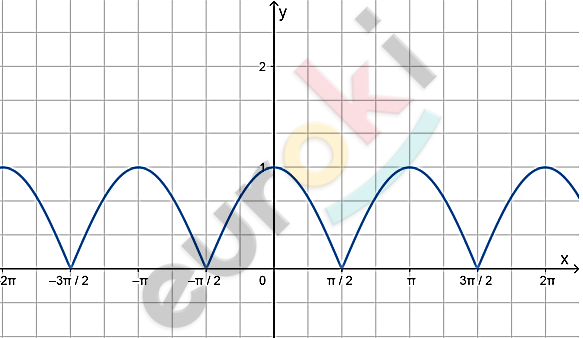
\[1)\ y = \left| \cos x \right|\]

\[\textbf{а)}\ D(x) = ( - \infty;\ + \infty);\]

\[\textbf{б)}\ - 1 \leq \cos x \leq 1;\]

\[0 \leq \left| \cos x \right| \leq 1;\]

\[E(y) = \lbrack 0;\ 1\rbrack.\]

\[\textbf{в)}\ y(x + T) = y(x)\]

\[\left| \cos(x + T) \right| = \left| \cos x \right|\]

\[\left\{ \begin{matrix} \cos(x + T) = \cos x\text{\ \ \ \ } \\ \cos(x + T) = - \cos x \\ \end{matrix} \right.\ \text{\ \ \ }\]

\[\left\{ \begin{matrix} T = 2\pi\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \cos(x + T) = \cos(x + \pi) \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} T = 2\pi \\ T = \pi\ \ \\ \end{matrix} \right.\ \]

\[T = \pi.\]

\[\textbf{г)}\ Функция\ четная:\]

\[y( - x) = \left| \cos( - x) \right| =\]

\[= \left| \cos x \right| = y(x).\]

\[\textbf{д)}\ \left| \cos x \right| = 0;\]

\[x = \arccos 0 + \pi n = \frac{\pi}{2} + \pi n.\]

\[\textbf{е)}\ Максимальные\ значения:\]

\[\left| \cos x \right| = 1\]

\[\cos x = \pm 1\]

\[x_{1} = \pi - \arccos 1 + 2\pi n =\]

\[= \pi + 2\pi n;\]

\[x_{2} = \arccos 1 + 2\pi n = 2\pi n;\]

\[x = \pi.\]

\[\textbf{ж)}\ Минимальные\ значения:\]

\[x = \frac{\pi}{2} + \pi n.\]

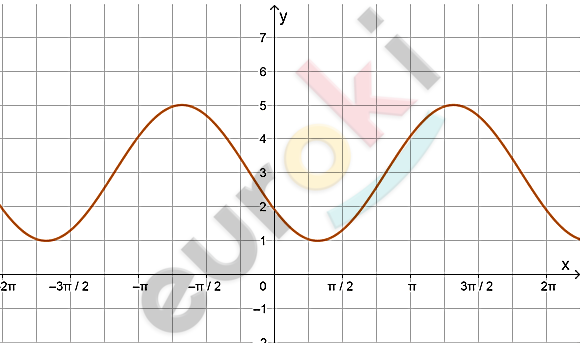
\[2)\ y = 3 - 2\cos(x - 1)\ \]

\[\textbf{а)}\ D(x) = ( - \infty;\ + \infty);\]

\[\textbf{б)}\ - 1 \leq \cos(x - 1) \leq 1;\]

\[- 2 \leq - 2\cos(x - 1) \leq 2;\]

\[1 \leq 3 - 2\cos(x - 1) \leq 5;\]

\[E(y) = \lbrack 1;\ 5\rbrack.\]

\[\textbf{в)}\ y(x + T) = y(x);\]

\[3 - 2\cos(x + T - 1) = 3 - 2\cos x;\]

\[T - 1 = 2\pi;\]

\[T = 2\pi + 1.\]

\[\textbf{г)}\ Ни\ четная,\ ни\ нечетная:\]

\[y( - x) = 3 - 2\cos( - x - 1) =\]

\[= 3 - 2\cos(x + 1).\]

\[\textbf{д)}\ 3 - 2\cos(x - 1) = 0\]

\[нет\ корней.\]

\[\textbf{е)}\ Максимальные\ значения:\]

\[3 - 2\cos(x - 1) = 5;\]

\[- 2\cos(x - 1) = 2;\]

\[\cos(x - 1) = - 1;\]

\[x - 1 = \pi - \arccos 1 + 2\pi n\]

\[x - 1 = \pi + 2\pi n;\]

\[x = \pi + 1 + 2\pi n.\]

\[\textbf{ж)}\ Минимальные\ значения:\]

\[3 - 2\cos(x - 1) = 1;\]

\[- 2\cos(x - 1) = - 2;\]

\[\cos(x - 1) = 1;\]

\[x - 1 = \arccos 1 + 2\pi n = 2\pi n;\]

\[x = 1 + 2\pi n.\]