Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 710

\[\boxed{\mathbf{710}\mathbf{.}}\]

\[y = \cos x:\]

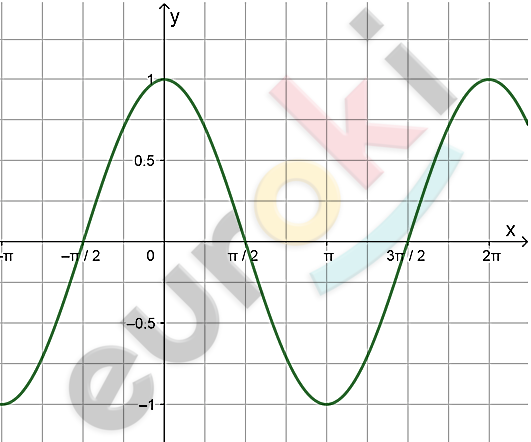
\[1)\ \left\lbrack \frac{\pi}{2};\ \frac{3\pi}{2} \right\rbrack:\]

\[возрастает\ на\ отрезке\ \left\lbrack \pi;\ \frac{3\pi}{2} \right\rbrack;\ \]

\[убывает\ на\ отрезке\ \left\lbrack \frac{\pi}{2};\ \pi \right\rbrack.\]

\[2)\ \left\lbrack - \frac{\pi}{2};\ \frac{\pi}{2} \right\rbrack:\]

\[возрастает\ на\ отрезке\ \left\lbrack - \frac{\pi}{2};\ 0 \right\rbrack;\ \]

\[убывает\ на\ отрезке\ \left\lbrack 0;\ \frac{\pi}{2} \right\rbrack.\]

\[3)\ \left\lbrack 0;\ \frac{3\pi}{2} \right\rbrack:\]

\[возрастает\ на\ отрезке\ \left\lbrack \pi;\ \frac{3\pi}{2} \right\rbrack;\ \]

\[убывает\ на\ отрезке\ \lbrack 0;\ \pi\rbrack.\]

\[4)\ \left\lbrack - \pi;\ \frac{\pi}{2} \right\rbrack:\]

\[возрастает\ на\ отрезке\ \lbrack - \pi;\ 0\rbrack;\ \]

\[убывает\ на\ отрезке\ \left\lbrack 0;\ \frac{\pi}{2} \right\rbrack.\]