Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре и начала математического анализа 11 класс Алимов Задание 542
Задание 542
\[\boxed{\mathbf{542}\mathbf{.}}\]
\[1)\cos^{4}a - \sin^{4}a + \sin{2a} =\]
\[= \sqrt{2}\cos\left( 2a - \frac{\pi}{4} \right)\]
\[\cos{2a} \bullet 1 + \cos\left( \frac{\pi}{2} - 2a \right) =\]
\[= \sqrt{2}\cos\left( 2a - \frac{\pi}{4} \right)\]
\[= \sqrt{2}\cos\left( 2a - \frac{\pi}{4} \right)\]
\[2 \bullet \cos\frac{\pi}{4} \bullet \cos\left( 2a - \frac{\pi}{4} \right) =\]
\[= \sqrt{2}\cos\left( 2a - \frac{\pi}{4} \right)\]
\[2 \bullet \frac{\sqrt{2}}{2} \bullet \cos\left( 2a - \frac{\pi}{4} \right) =\]
\[= \sqrt{2}\cos\left( 2a - \frac{\pi}{4} \right)\]
\[\sqrt{2}\cos\left( 2a - \frac{\pi}{4} \right) =\]
\[= \sqrt{2}\cos\left( 2a - \frac{\pi}{4} \right)\]
\[Что\ и\ требовалось\ доказать.\]
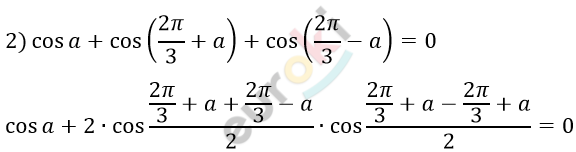
\[\cos a + 2 \bullet \cos\frac{2\pi}{3} \bullet \cos a = 0\]
\[\cos a + 2 \bullet \cos\left( \pi - \frac{\pi}{3} \right) \bullet \cos a = 0\]
\[\cos a - 2 \bullet \cos\frac{\pi}{3} \bullet \cos a = 0\]
\[\cos a - 2 \bullet \frac{1}{2} \bullet \cos a = 0\]
\[\cos a - \cos a = 0\]
\[0 = 0\]
\[Что\ и\ требовалось\ доказать.\]
\[3)\ \frac{\sin{2a} + \sin{5a} - \sin{3a}}{\cos a + 1 - 2\sin^{2}{2a}} =\]
\[= 2\sin a\]
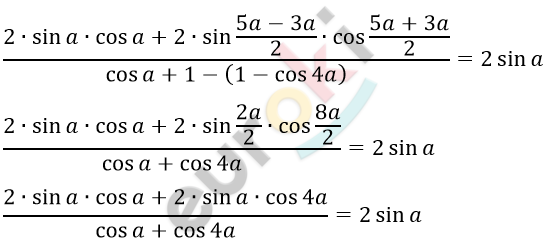
\[\frac{2\sin a\left( \cos a + \cos{4a} \right)}{\cos a + \cos{4a}} = 2\sin a\]
\[2\sin a = 2\sin a\]
\[Что\ и\ требовалось\ доказать.\]
