Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 402

\[\boxed{\mathbf{402.}}\]

\[1)\ 3 + 2\log_{x + 1}3 = 2\log_{3}(x + 1)\]

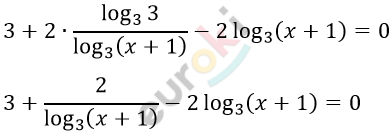
\[Пусть\ y = \log_{3}(x + 1):\]

\[3 + \frac{2}{y} - 2y = 0\ \ \ \ \ | \bullet y\]

\[3y + 2 - 2y^{2} = 0\]

\[2y^{2} - 3y - 2 = 0\]

\[D = 3^{2} + 4 \bullet 2 \bullet 2 = 9 + 16 = 25\]

\[y_{1} = \frac{3 - 5}{2 \bullet 2} = - \frac{2}{4} = - \frac{1}{2};\]

\[y_{2} = \frac{3 + 5}{2 \bullet 2} = \frac{8}{4} = 2.\]

\[1)\ \log_{3}(x + 1) = - \frac{1}{2}\]

\[\log_{3}(x + 1) = \log_{3}3^{- \frac{1}{2}}\]

\[x + 1 = 3^{- \frac{1}{2}}\]

\[x = \frac{1}{3^{\frac{1}{2}}} - 1\]

\[x = \frac{1}{\sqrt{3}} - 1.\]

\[2)\ \log_{3}(x + 1) = 2\]

\[\log_{3}(x + 1) = \log_{3}3^{2}\]

\[x + 1 = 3^{2}\]

\[x = 9 - 1\]

\[x = 8.\]

\[имеет\ смысл\ при:\]

\[x + 1 > 0 \Longrightarrow x > - 1.\]

\[Ответ:\ \ x_{1} = \frac{1}{\sqrt{3}} - 1;\ \ x_{2} = 8.\ \]

\[2)\ 1 + 2\log_{x + 2}5 = \log_{5}(x + 2)\]

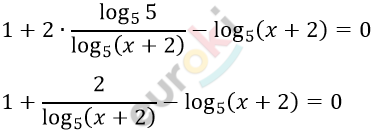
\[Пусть\ y = \log_{5}(x + 2):\]

\[1 + \frac{2}{y} - y = 0\ \ \ \ \ | \bullet y\]

\[y + 2 - y^{2} = 0\]

\[y^{2} - y - 2 = 0\]

\[D = 1^{2} + 4 \bullet 2 = 1 + 8 = 9\]

\[y_{1} = \frac{1 - 3}{2} = - 1;\text{\ \ }\]

\[y_{2} = \frac{1 + 3}{2} = 2.\]

\[1)\ \log_{5}(x + 2) = - 1\]

\[\log_{5}(x + 2) = \log_{5}5^{- 1}\]

\[x + 2 = 5^{- 1}\]

\[x = \frac{1}{5} - 2\]

\[x = 0,2 - 2\]

\[x = - 1,8.\]

\[2)\ \log_{5}(x + 2) = 2\]

\[\log_{5}(x + 2) = \log_{5}5^{2}\]

\[x + 2 = 5^{2}\]

\[x = 25 - 2\]

\[x = 23.\]

\[имеет\ смысл\ при:\]

\[x + 2 > 0 \Longrightarrow x > - 2.\]

\[Ответ:\ \ x_{1} = - 1,8;\ \ x_{2} = 23.\]