Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 307

\[\boxed{\mathbf{307}\mathbf{.}}\]

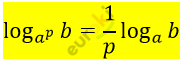
\[1)\log_{5}x = 2\log_{5}3 + 4\log_{25}2\]

\[\log_{5}x = \log_{5}3^{2} + 2\log_{5^{2}}2^{2}\]

\[\log_{5}x = \log_{5}9 + \log_{5}4\]

\[\log_{5}x = \log_{5}(9 \bullet 4)\]

\[\log_{5}x = \log_{5}36\]

\[Ответ:\ \ x = 36.\]

\[2)\log_{2}x - 2\log_{\frac{1}{2}}x = 9\]

\[\log_{2}x - 2\log_{2^{- 1}}x = \log_{2}2^{9}\]

\[\log_{2}x + 2\log_{2}x = \log_{2}512\]

\[3\log_{2}x = \log_{2}512\]

\[\log_{2}x^{3} = \log_{2}512\]

\[x^{3} = 512\]

\[x = 8\]

\[Ответ:\ \ x = 8.\]

\[3)\log_{3}x = 9\log_{27}8 - 3\log_{3}4\]

\[\log_{3}x = 3\log_{3^{3}}8^{3} - \log_{3}4^{3}\]

\[\log_{3}x = \log_{3}512 - \log_{3}64\]

\[\log_{3}x = \log_{3}\frac{512}{64}\]

\[\log_{3}x = \log_{3}8\]

\[Ответ:\ \ x = 8.\]

\[4)\log_{9}x^{2} + \log_{\sqrt{3}}x = 3\]

\[2\log_{3^{2}}x + \log_{3^{\frac{1}{2}}}x = \log_{3}3^{3}\]

\[\log_{3}x + 2\log_{3}x = \log_{3}27\]

\[3\log_{3}x = \log_{3}27\]

\[\log_{3}x^{3} = \log_{3}27\]

\[x^{3} = 27\ \]

\[x = 3\]

\[Ответ:\ \ x = 3.\]

\[5)\log_{2}x + \log_{8}x = 8\]

\[\log_{2}x + \log_{2^{3}}x = \log_{2}2^{8}\]

\[\log_{2}x + \frac{1}{3}\log_{2}x = \log_{2}256\]

\[\frac{4}{3}\log_{2}x = \log_{2}256\]

\[\log_{2}x^{\frac{4}{3}} = \log_{2}256\]

\[x^{\frac{4}{3}} = 256\]

\[x^{\frac{1}{3}} = 4\ \]

\[x = 64\]

\[Ответ:\ \ x = 64.\]

\[6)\log_{4}x - \log_{16}x = \frac{1}{4}\]

\[\log_{4}x - \log_{4^{2}}x = \log_{4}4^{\frac{1}{4}}\]

\[\log_{4}x - \frac{1}{2}\log_{4}x = \log_{4}2^{\frac{1}{2}}\]

\[\frac{1}{2}\log_{4}x = \frac{1}{2}\log_{4}2\]

\[\log_{4}x = \log_{4}2\]

\[Ответ:\ \ x = 2.\]