Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 300

\[\boxed{\mathbf{300}\mathbf{.}}\]

\[1)\log_{\sqrt{3}}50\]

\[\log_{3}15 = a\ \ и\ \log_{3}10 = b:\]

\[\log_{\sqrt{3}}50 = \log_{3^{\frac{1}{2}}}50 =\]

\[= 1\ :\frac{1}{2} \bullet \log_{3}50 =\]

\[= 2\log_{3}(5 \bullet 10) =\]

\[= 2\left( \log_{3}5 + \log_{3}10 \right) =\]

\[= 2\left( 1 + \log_{3}5 + \log_{3}10 - 1 \right) =\]

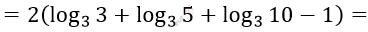
\[= 2\left( \log_{3}(3 \bullet 5) + \log_{3}10 - 1 \right) =\]

\[= 2\left( \log_{3}15 + \log_{3}10 - 1 \right) =\]

\[= 2(a + b - 1)\]

\[Ответ:\ \ 2(a + b - 1).\]

\[2)\log_{4}1250\]

\[\log_{2}5 = a:\]

\[\log_{4}1250 = \log_{2^{2}}1250 =\]

\[= \frac{1}{2}\log_{2}(625 \bullet 2) =\]

\[= \frac{1}{2}\left( \log_{2}625 + \log_{2}2 \right) =\]

\[= \frac{1}{2}\left( \log_{2}5^{4} + 1 \right) =\]

\[= \frac{1}{2}\left( 4\log_{2}5 + 1 \right) =\]

\[= \frac{1}{2}(4a + 1) = 2a + \frac{1}{2}\]

\[Ответ:\ \ 2a + \frac{1}{2}\text{.\ }\]