Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 205

\[\boxed{\mathbf{205}\mathbf{.}}\]

\[1)\ y = 2^{|x|};\]

\[Функция\ является\ четной:\]

\[y( - x) = 2^{| - x|} = 2^{|x|} = y(x).\]

\[Если\ x \geq 0,\ то\ y = 2^{x}:\]

\[- \ область\ определения:\ \ x \in R;\]

\[- \ множество\ значений:\ \ y \geq 1;\]

\[- \ функция\ возрастает\ \]

\[на\ (0;\ + \infty)\ и\ убывает\ \]

\[на\ ( - \infty;\ 0).\]

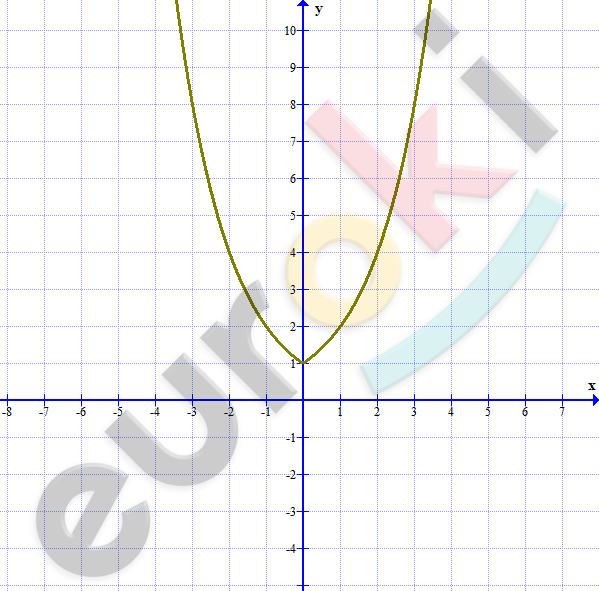
\[2)\ y = \left( \frac{1}{3} \right)^{|x|}\]

\[Функция\ четная:\]

\[y( - x) = \left( \frac{1}{3} \right)^{| - x|} = \left( \frac{1}{3} \right)^{|x|} = y(x).\]

\[Если\ x \geq 0,\ тогда\ y = \left( \frac{1}{3} \right)^{x}:\]

\[- \ область\ определения:\ \ x \in R;\]

\[- \ множество\ значений:\ \ \]

\[0 < y \leq 1;\]

\[- \ функция\ возрастает\ \]

\[на\ ( - \infty;\ 0)\ и\ убывает\ \]

\[на\ (0;\ + \infty).\]

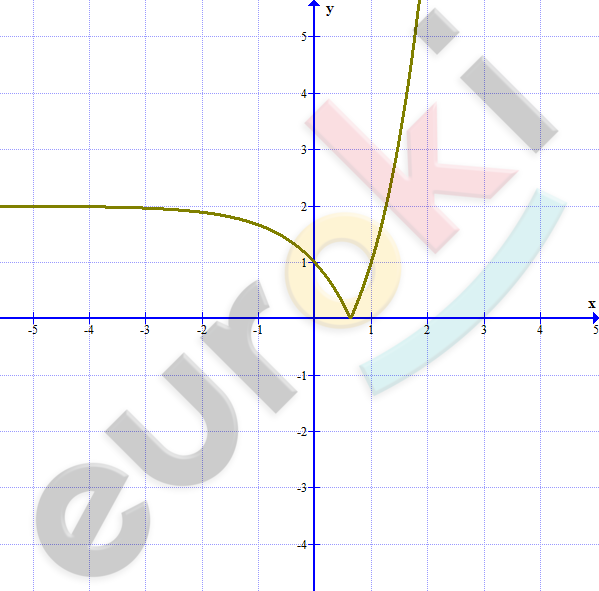
\[3)\ y = \left| 3^{x} - 2 \right|\]

\[y = 3^{x}:\]

\[- \ область\ определения:\ \ x \in R;\]

\[- \ множество\ значений:\ \ y > 0;\]

\[- \ функция\ возрастает,\ \]

\[так\ как\ 3 > 1.\]

\[Построим\ график\ \]

\[функции\ y = 3^{x}\ и\ сдвинем\ его\ \]

\[вдоль\ оси\ ординат\ \]

\[на\ 2\ единицы\ вниз,\ а\ затем\ \]

\[отразим\ его\ часть,\ \]

\[находящуюсяьпод\ осью\ \]

\[ординат.\]

\[4)\ y = 2 - 3^{x}\]

\[y = 3^{x}:\]

\[- \ область\ определения:\ \ x \in R;\]

\[- \ множество\ значений:\ \ y > 0;\]

\[- \ функция\ возрастает,\ \]

\[так\ как\ 3 > 1.\]

\[Построим\ график\ \]

\[функции\ y = 3^{x}\ и\ отразим\ его\ \]

\[относительно\ оси\ ординат,\ \]

\[а\ затем\ осуществим\ сдвиг\ \]

\[вдоль\ нее\ на\ 2\ единицы\ вверх.\]