Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 201

\[\boxed{\mathbf{201}\mathbf{.}}\]

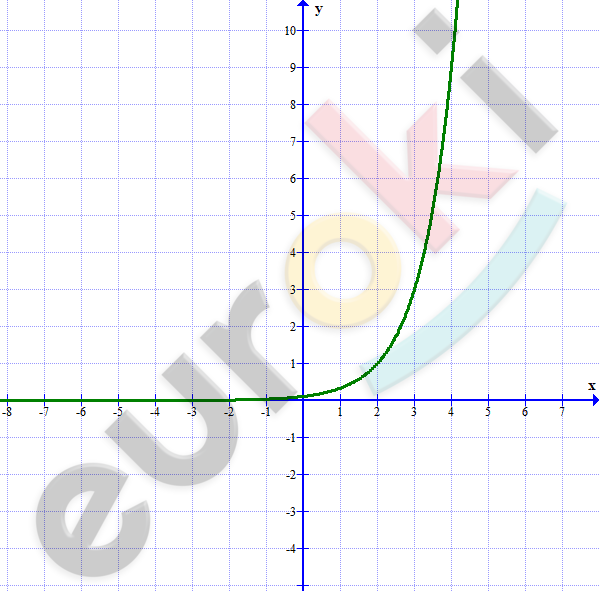
\[1)\ y = 3^{x} - 2;\]

\[y = 3^{x}:\]

\[- \ область\ определения:\ \ x \in R;\]

\[- \ множество\ значений:\ \ y > 0;\]

\[- \ функция\ возрастает,\ \]

\[так\ как\ 3 > 1.\]

\[Построим\ график\ функции\ \]

\[y = 3^{x}\ и\ сдвинем\ его\ вдоль\ оси\ \]

\[\ ординат\ на\ 2\ единицы\ вниз.\]

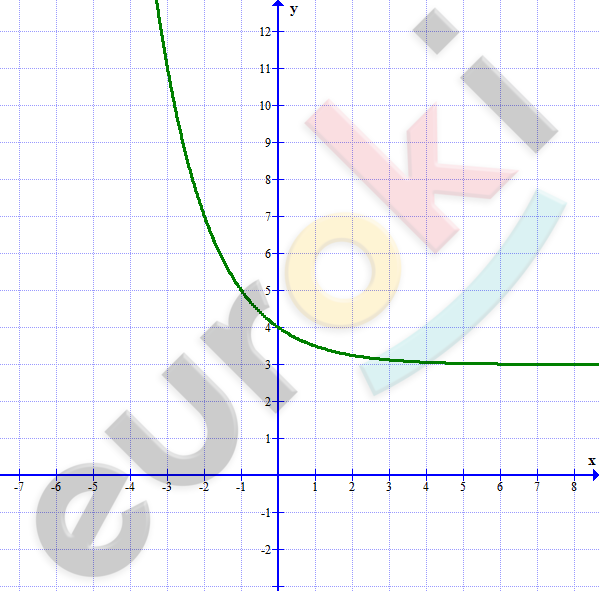
\[2)\ y = \left( \frac{1}{2} \right)^{x} + 3\]

\[y = \left( \frac{1}{2} \right)^{x}:\]

\[- \ область\ определения:\ \ x \in R;\]

\[- \ множество\ значений:\ \ y > 0;\]

\[- \ функция\ убывает,\ \]

\[так\ как\ 0 < \frac{1}{2} < 1.\]

\[Построим\ график\ \]

\[функции\ y = \left( \frac{1}{2} \right)^{x}\ и\ сдвинем\ \]

\[его\ вдоль\ оси\ \ ординат\ \]

\[на\ 3\ единицы\ вверх.\]

\[3)\ y = 2^{x + 1};\]

\[\ y = 2^{x}:\]

\[- \ область\ определения:\ \ x \in R;\]

\[- \ множество\ значений:\ \ y > 0;\]

\[- \ функция\ возрастает,\ \]

\[так\ как\ 2 > 1.\]

\[Построим\ график\ функции\ \]

\[y = 2^{x}\ и\ сдвинем\ его\ вдоль\ оси\ \]

\[абсцисс\ на\ 1\ единицу\ влево.\]

\[4)\ y = 3^{x - 2}\]

\[y = 3^{x}:\]

\[- \ область\ определения:\ \ x \in R;\]

\[- \ множество\ значений:\ \ y > 0;\]

\[- \ функция\ возрастает,\ \]

\[так\ как\ 3 > 1.\]

\[Построим\ график\ функции\ \]

\[y = 3^{x}\ и\ сдвинем\ его\ вдоль\ оси\ \]

\[абсцисс\ на\ 2\ единицы\ вправо.\]