Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 1584

\[\boxed{\mathbf{1584}\mathbf{.}}\]

\[- 1 \leq x \leq 1:\]

\[\arcsin x + \arccos x = C\]

\[\arcsin x = C - \arccos x\]

\[\sin\left( \arcsin x \right) = \sin\left( C - \arccos x \right)\]

\[x = \sin\left( C - \arccos x \right)\]

\[x = \sin C \bullet \cos\left( \arccos x \right) - \cos C \bullet \sin\left( \arccos x \right)\]

\[x = x \bullet \sin C - \sqrt{1 - \cos^{2}\left( \arccos x \right)} \bullet \cos C\]

\[x - x \bullet \sin C = - \sqrt{1 - x^{2}} \bullet \cos C\]

\[x\left( \sin C - 1 \right) = \sqrt{1 - x^{2}} \bullet \cos C\]

\[x^{2}\left( \sin^{2}C - 2\sin C + 1 \right) =\]

\[= \left( 1 - x^{2} \right) \bullet \cos^{2}C\]

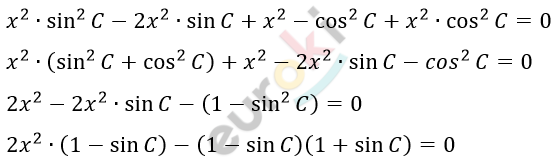
\[\left( 1 - \sin C \right)\left( 2x^{2} - \left( 1 + \sin C \right) \right) = 0\]

\[Имеет\ решение\ при:\]

\[1 - \sin C = 0\]

\[\sin C = 1\]

\[C = \arcsin 1 + 2\pi n\]

\[C = \frac{\pi}{2} + 2\pi n.\]

\[При\ этом:\]

\[- \frac{\pi}{2} \leq \arcsin x \leq \frac{\pi}{2};\ \]

\[0 \leq \arccos x \leq \pi;\]

\[- \frac{\pi}{2} \leq \arcsin x + \arccos x \leq \frac{3\pi}{2}.\]

\[Существует\ значение\ C = \frac{\pi}{2},\ \]

\[при\ котором\ верно\ данное\]

\[равенство,\ и\ при\ этом\ только\]

\[одно.\]

\[Что\ и\ требовалось\ доказать.\]

\[Ответ:\ \ C = \frac{\pi}{2}.\]