Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 1580

\[\boxed{\mathbf{1580}\mathbf{.}}\]

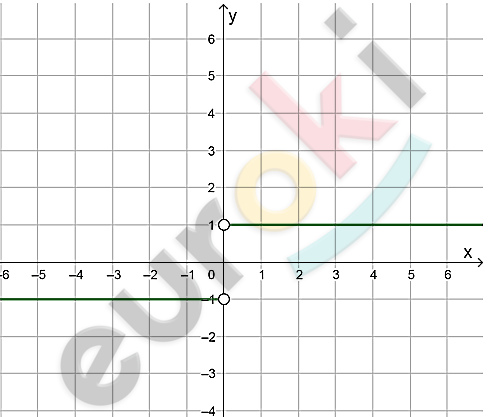
\[1)\ y = \frac{\sqrt{x^{2}}}{x} = \frac{|x|}{x}\]

\[x \neq 0;\]

\[D(x) = ( - \infty;\ 0) \cup (0;\ + \infty).\]

\[x < 0:\]

\[y = - \frac{x}{x} = - 1.\]

\[x > 0:\]

\[y = \frac{x}{x} = 1.\]

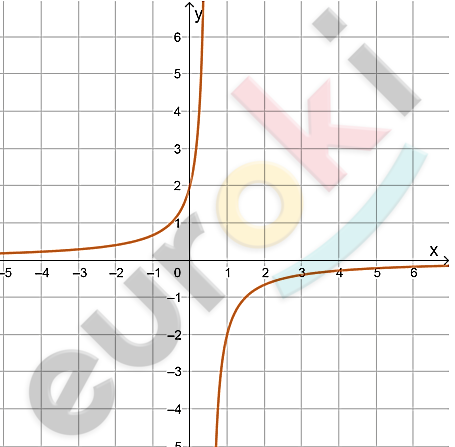
\[2)\ y = \frac{2}{1 - 2x}\]

\[1 - 2x \neq 0\]

\[2x \neq 1\]

\[x \neq 0,5\]

\[D(x) = ( - \infty;\ 0,5) \cup (0,5;\ + \infty).\]

\[f^{'}(x) = 2 \bullet (1 - 2x)^{- 1} =\]

\[= 2 \bullet ( - 1) \bullet ( - 2) \bullet (1 - 2x)^{- 2} =\]

\[= \frac{4}{(1 - 2x)^{2}} > 0.\]

\[Функция\ возрастает\ на\ всей\ \]

\[области\ определения.\]

\[\lim_{x \rightarrow \infty}\frac{2}{1 - 2x} = \lim_{x \rightarrow \infty}\frac{\frac{2}{x}}{\frac{1}{x} - 2} =\]

\[= \frac{0}{0 - 2} = 0;\]

\[E(y) = ( - \infty;\ 0) \cup (0;\ + \infty).\]

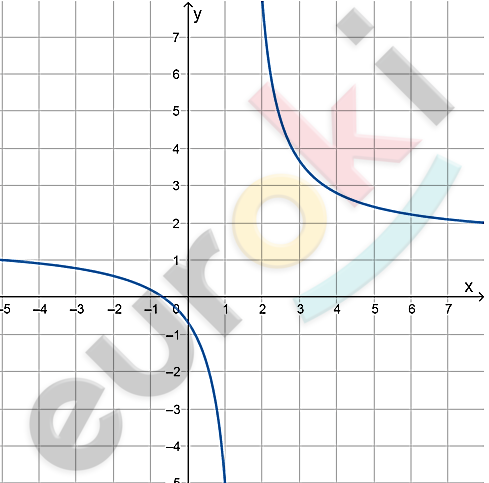
\[3)\ y = \frac{3x + 2}{2x - 3}\]

\[2x - 3 \neq 0\]

\[2x = 3\]

\[x = 1,5;\]

\[D(x) = ( - \infty;\ 1,5) \cup (1,5;\ + \infty).\]

\[f^{'}(x) =\]

\[= \frac{(3x + 2)^{'} \bullet (2x - 3) - (3x + 2) \bullet (2x - 3)^{'}}{(2x - 3)^{2}} =\]

\[= \frac{3(2x - 3) - 2(3x + 2)}{(2x - 3)^{2}} =\]

\[= \frac{6x - 9 - 6x - 4}{(2x - 3)^{2}} =\]

\[= \frac{- 13}{(2x - 3)^{2}} < 0;\]

\[Функция\ убывает\ на\ всей\ \]

\[области\ определения.\]

\[\lim_{x \rightarrow \infty}\frac{3x + 2}{2x - 3} = \lim_{x \rightarrow \infty}\frac{3 + \frac{2}{x}}{2 - \frac{3}{x}} =\]

\[= \frac{3 + 0}{2 - 0} = 1,5;\]

\[E(y) = ( - \infty;\ 1,5) \cup (1,5;\ + \infty).\]

\[4)\ y = \frac{2x}{2 - |x|}\]

\[Функция\ нечетная:\]

\[y( - x) = \frac{2 \bullet ( - x)}{2 - | - x|} =\]

\[= - \frac{2x}{2 - |x|} = - y(x).\]

\[2 - |x| \neq 0\]

\[|x| \neq 2\]

\[x \neq \pm 2;\]

\[D(x) = ( - \infty;\ - 2) \cup ( - 2;\ 2) \cup (2;\ + \infty).\]

\[x > 0:\]

\[y = \frac{2x}{2 - x}.\]

\[f^{'}(x) = \frac{(2x)^{'} \bullet (2 - x) - 2x \bullet (2 - x)'}{(2 - x)^{2}} =\]

\[= \frac{2(2 - x) + 2x}{(2 - x)^{2}} = \frac{4 - 2x + 2x}{(2 - x)^{2}} =\]

\[= \frac{4}{(2 - x)^{2}} > 0.\]

\[Функция\ возрастает\ на\ всей\ \]

\[области\ определения.\]

\[\lim_{x \rightarrow \infty}\frac{2x}{2 - x} = \lim_{x \rightarrow \infty}\frac{2}{\frac{2}{x} - 1} =\]

\[= \frac{2}{0 - 1} = - 2.\]

\[E(y) = ( - \infty;\ + \infty).\]