Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 1371

\[\boxed{\mathbf{1371}\mathbf{.}}\]

\[1)\ \sqrt{3}\sin{2x} - \cos{2x} = \sqrt{3}\]

\[\sqrt{3} \bullet \left( \sin{2x} - 1 \right) - \cos{2x} = 0\]

\[\cos x - \sin x = 0\ \ \ \ \ |\ :\cos x\]

\[1 - tg\ x = 0\]

\[tg\ x = 1\]

\[x = arctg\ 1 + \pi n = \frac{\pi}{4} + \pi n.\]

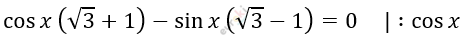
\[\left( \sqrt{3} + 1 \right) - tg\ x\left( \sqrt{3} - 1 \right) = 0\]

\[\text{tg\ x}\left( \sqrt{3} - 1 \right) = \sqrt{3} + 1\]

\[tg\ x = \frac{\sqrt{3} + 1}{\sqrt{3} - 1}\]

\[x = arctg\frac{\sqrt{3} + 1}{\sqrt{3} - 1} + \pi n.\]

\[Ответ:\ \ \frac{\pi}{4} + \pi n;\ \ \]

\[\text{arctg}\frac{\sqrt{3} + 1}{\sqrt{3} - 1} + \pi n.\]

\[2)\ 6\sin x + 5\cos x = 6\]

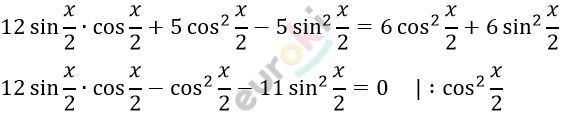
\[12\ tg\frac{x}{2} - 1 - 11\ tg^{2}\frac{x}{2} = 0\]

\[y = tg\frac{x}{2}:\]

\[12y - 1 - 11y^{2} = 0\]

\[11y^{2} - 12y + 1 = 0\]

\[D = 144 - 44 = 100\]

\[y_{1} = \frac{12 - 10}{2 \bullet 11} = \frac{2}{22} = \frac{1}{11};\]

\[y_{2} = \frac{12 + 10}{2 \bullet 11} = \frac{22}{22} = 1.\]

\[1)\ tg\frac{x}{2} = \frac{1}{11}\]

\[\frac{x}{2} = arctg\frac{1}{11} + \pi n\]

\[x = 2 \bullet \left( \text{arctg}\frac{1}{11} + \pi n \right)\]

\[x = 2\ arctg\frac{1}{11} + 2\pi n.\]

\[2)\ tg\frac{x}{2} = 1\]

\[\frac{x}{2} = arctg\ 1 + \pi n = \frac{\pi}{4} + \pi n\]

\[x = 2 \bullet \left( \frac{\pi}{4} + \pi n \right) = \frac{\pi}{2} + 2\pi n.\]

\[Ответ:\ \ 2\ arctg\frac{1}{11} + 2\pi n;\ \ \]

\[\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\frac{\pi}{2} + 2\pi n.\]