Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре и начала математического анализа 11 класс Алимов Задание 137
Задание 137
\[\boxed{\mathbf{137.}}\]
\[1)\ y = 3x - 1;\]
\[Основная\ функция:\]
\[- \ область\ определения:\ \ x \in R;\]
\[- \ множество\ значений:\ \ y \in R.\]
\[Обратная\ функция:\]
\[x = 3y - 1\]
\[3y = x + 1\]
\[y = \frac{x + 1}{3}.\]
\[- \ область\ определения:\ \ x \in R;\]
\[- \ множество\ значений:\ \ y \in R.\]
\[2)\ y = \frac{2x - 1}{3}\]
\[Основная\ функция:\]
\[- \ область\ определения:\ \ x \in R;\]
\[- \ множество\ значений:\ \ y \in R.\]
\[Обратная\ функция:\]
\[x = \frac{2y - 1}{3}\]
\[3x = 2y - 1\]
\[2y = 3x + 1\]
\[y = \frac{3x + 1}{2}.\]
\[- \ область\ определения:\ \ x \in R;\]
\[- \ множество\ значений:\ \ y \in R.\]
\[3)\ y = x^{2} - 1\ при\ x \geq 0;\]
\[Основная\ функция:\]
\[- \ область\ определения:\ \ x \geq 0;\]
\[- \ множество\ значений:\ \ y \geq - 1.\]
\[Обратная\ функция:\]
\[x = y^{2} - 1\]
\[y^{2} = x + 1\]
\[y = \sqrt{x + 1}.\]
\[- \ область\ определения:\ \ \]
\[x \geq - 1;\]
\[- \ множество\ значений:\ \ y \geq 0.\]
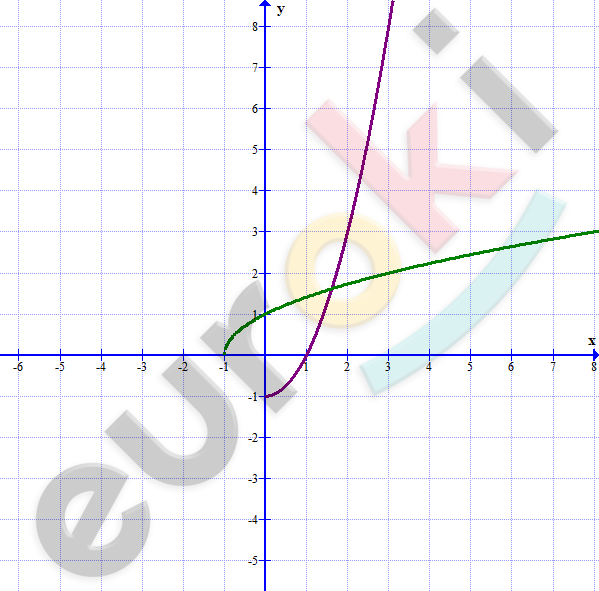
\[4)\ y = (x - 1)^{2}\ при\ x \geq 1\]
\[Основная\ функция:\]
\[- \ область\ определения:\ \ x \geq 1;\]
\[- \ множество\ значений:\ \ y \geq 0.\]
\[Обратная\ функция:\]
\[x = (y - 1)^{2}\]
\[\sqrt{x} = y - 1\]
\[y = \sqrt{x} + 1.\]
\[- \ область\ определения:\ \ x \geq 0;\]
\[- \ множество\ значений:\ \ y \geq 1.\]
\[5)\ y = x^{3} - 2\]
\[Основная\ функция:\]
\[- \ область\ определения:\ \ x \in R;\]
\[- \ множество\ значений:\ \ y \in R.\]
\[Обратная\ функция:\]
\[x = y^{3} - 2\]
\[y^{3} = x + 2\]
\[y = \sqrt[3]{x + 2}.\]
\[- \ область\ определения:\ \ x \in R;\]
\[- \ множество\ значений:\ \ y \in R.\]
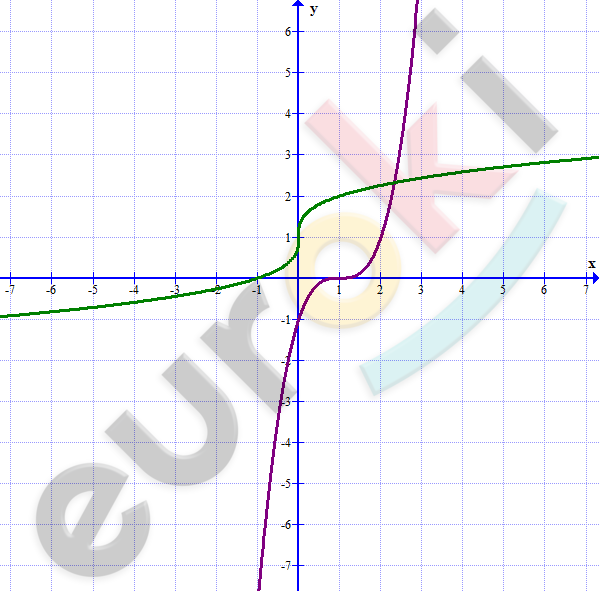
\[6)\ y = (x - 1)^{3}\]
\[Основная\ функция:\]
\[- \ область\ определения:\ \ x \in R;\]
\[- \ множество\ значений:\ \ y \in R.\]
\[Обратная\ функция:\]
\[x = (y - 1)^{3}\]
\[\sqrt[3]{x} = y - 1\]
\[y = \sqrt[3]{x} + 1.\]
\[- \ область\ определения:\ \ x \in R;\]
\[- \ множество\ значений:\ \ y \in R.\]
\[7)\ y = \sqrt{x - 1};\]
\[Основная\ функция:\]
\[- \ область\ определения:\ \ x \geq 1;\]
\[- \ множество\ значений:\ \ y \geq 0.\]
\[Обратная\ функция:\]
\[x = \sqrt{y - 1}\]
\[x^{2} = y - 1\]
\[y = x^{2} + 1.\]
\[- область\ определения:\ \ x \geq 0;\]
\[- множество\ значений:\ \ y \geq 1.\]
\[8)\ y = \sqrt{x} + 1;\]
\[Основная\ функция:\]
\[- \ область\ определения:\ \ x \geq 0;\]
\[- \ множество\ значений:\ \ y \geq 1.\]
\[Обратная\ функция:\]
\[x = \sqrt{y} + 1\]
\[\sqrt{y} = x - 1\]
\[y = (x - 1)^{2}.\]
\[- \ область\ определения:\ \ x \geq 1;\]
\[- \ множество\ значений:\ \ y \geq 0.\]
