Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре и начала математического анализа 11 класс Алимов Задание 129
Задание 129
\[\boxed{\mathbf{129.}}\]
\[1)\ y = |x|^{\frac{1}{3}}\]
\[Функция\ является\ четной:\]
\[y( - x) = | - x|^{\frac{1}{3}} = |x|^{\frac{1}{3}} = y(x).\]
\[Если\ x \geq 0,\ тогда\ y = x^{\frac{1}{3}}:\]
\[- \ область\ определения:\ \ x \in R;\]
\[- \ множество\ значений:\ \ y \geq 0;\]
\[- \ функция\ убывает\ на\ ( - \infty;\ 0)\ \]
\[и\ возрастает\ на\ (0;\ + \infty);\]
\[- \ функция\ ограничена\ снизу.\]
\[2)\ y = |x|^{5}\]
\[Функция\ является\ четной:\]
\[y( - x) = | - x|^{5} = |x|^{5} = y(x).\]
\[Если\ x \geq 0,\ тогда\ y = x^{5}:\]
\[- \ область\ определения:\ \ x \in R;\]
\[- \ множество\ значений:\ \ y \geq 0;\]
\[- \ функция\ убывает\ на\ ( - \infty;\ 0)\ \]
\[и\ возрастает\ на\ (0;\ + \infty);\]
\[- \ функция\ ограничена\ снизу.\]
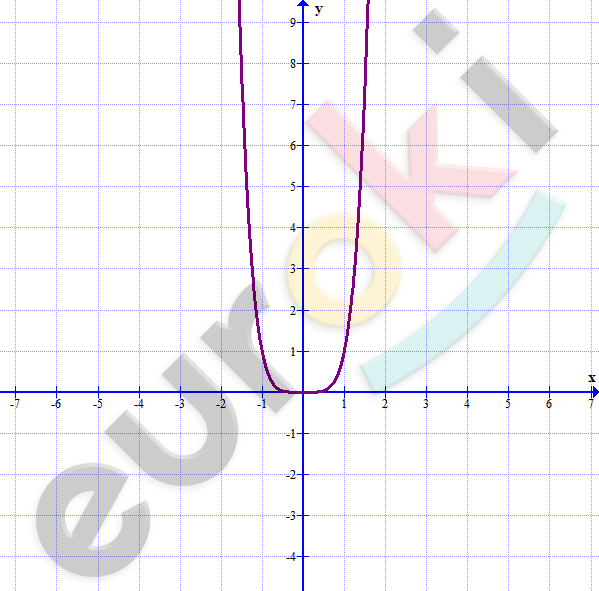
\[3)\ y = |x|^{3} + 1;\]
\[Функция\ является\ четной:\]
\[y( - x) = | - x|^{3} + 1 = |x|^{3} + 1 =\]
\[= y(x).\]
\[Если\ x \geq 0,\ тогда\ y = x^{3} + 1:\]
\[- \ область\ определения:\ \ x \in R;\]
\[- \ множество\ значений:\ \ y \geq 1;\]
\[- \ функция\ убывает\ на\ ( - \infty;\ 0)\ \]
\[и\ возрастает\ на\ (0;\ + \infty);\]
\[- \ функция\ ограничена\ снизу.\]
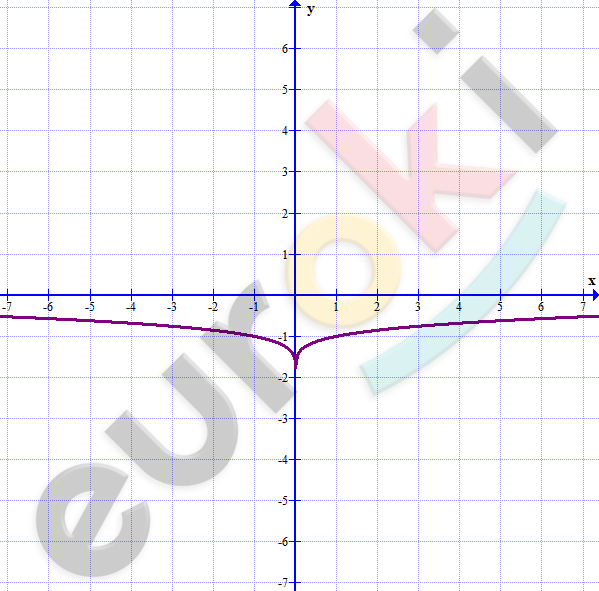
\[4)\ y = |x|^{\frac{1}{5}} - 2;\]
\[Функция\ является\ четной:\]
\[y( - x) = | - x|^{\frac{1}{5}} - 2 = |x|^{\frac{1}{5}} - 2 =\]
\[= y(x).\]
\[Если\ x \geq 0,\ тогда\ y = x^{\frac{1}{5}} - 2:\]
\[- \ область\ определения:\ \ x \in R;\]
\[- \ множество\ значений:\ \]
\[y \geq \text{-}2;\]
\[- \ функция\ убывает\ на\ ( - \infty;\ 0)\ \]
\[и\ возрастает\ на\ (0;\ + \infty);\]
\[- \ функция\ ограничена\ снизу.\]
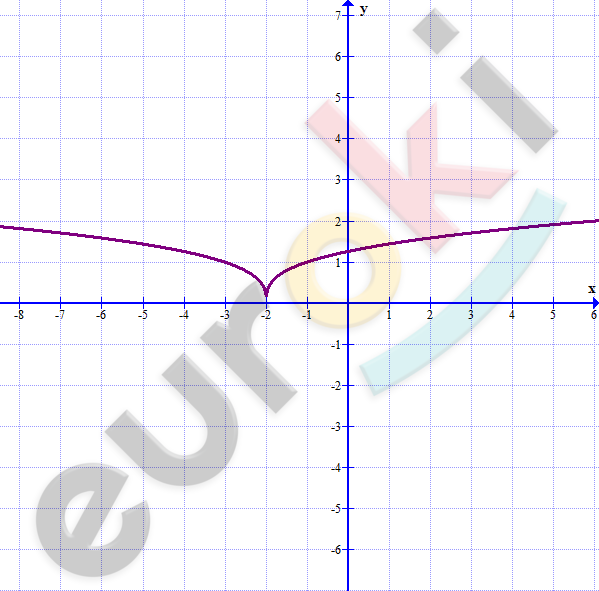
\[5)\ y = |x + 2|^{\frac{1}{3}};\]
\[График\ данной\ функции\ \]
\[явлется\ графиком\ функции\ \]
\[y = |x|^{\frac{1}{3}},\ сдвинутым\ вдоль\ оси\ \]
\[абсцисс\ на\ 2\ единицы\ влево.\]
\[Если\ x \geq - 2,\ тогда\ y = (x + 2)^{\frac{1}{3}}:\]
\[- \ область\ определения:\ \ x \in R;\]
\[- \ множество\ значений:\ \ y \geq 0;\]
\[- \ функция\ убывает\ \]
\[на\ ( - \infty;\ - 2)\ и\ возрастает\ \]
\[на\ ( - 2;\ + \infty);\]
\[- \ функция\ ограничена\ снизу.\]
\[6)\ y = |2x|^{- 3};\]
\[Функция\ является\ четной:\]
\[y( - x) = | - 2x|^{- 3} = |2x|^{- 3} =\]
\[= y(x).\]
\[Если\ x \geq 0,\ тогда\ y = (2x)^{- 3}:\]
\[- \ область\ определения:\ \ x \neq 0;\]
\[- \ множество\ значений:\ \ y > 0;\]
\[- \ функция\ возрастает\ \]
\[на\ ( - \infty;\ 0)\ и\ убывает\ \]
\[на\ (0;\ + \infty);\]
\[- \ функция\ ограничена\ снизу.\]
