Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 1022

\[\boxed{\mathbf{1022}\mathbf{.}}\]

\[1)\ y = - x^{2} + 4x - 3\ и\ \]

\[точки\ (1;\ 0)\ и\ (0;\ - 3)\]

\[\left\{ \begin{matrix} 0 = k \bullet 1 + b\ \ \ \\ - 3 = k \bullet 0 + b \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ \ \ }\left\{ \begin{matrix} 0 = k - 3 \\ b = - 3\ \ \ \ \\ \end{matrix} \right.\ \]

\[0 = k - 3 \rightarrow \ k = 3;\]

\[y = 3x - 3.\]

\[- x^{2} + 4x - 3 = 3x - 3\]

\[- x^{2} + 4x = 3x\]

\[x^{2} + 3x - 4x = 0\]

\[x^{2} - x = 0\]

\[x \bullet (x - 1) = 0\]

\[x_{1} = 0\ и\ x_{2} = 1.\]

\[S = \int_{0}^{1}{\left( \left( - x^{2} + 4x \right) - 3x \right)\text{\ dx}} =\]

\[= \left. \ \left( - \frac{x^{3}}{3} + 4 \bullet \frac{x^{2}}{2} - 3 \bullet \frac{x^{2}}{2} \right) \right|_{0}^{1} =\]

\[= \left. \ \left( - \frac{x^{3}}{3} + \frac{x^{2}}{2} \right) \right|_{0}^{1} =\]

\[= - \frac{1^{3}}{3} + \frac{1^{2}}{2} + \frac{0^{3}}{3} - \frac{0^{2}}{2} =\]

\[= - \frac{1}{3} + \frac{1}{2} = - \frac{2}{6} + \frac{3}{6} = \frac{1}{6}.\]

\[Ответ:\ \ \frac{1}{6}.\]

\[2)\ y = - x^{2}\text{\ \ }и\ \ y = - 2\]

\[Перенесем\ обе\ функции\ \]

\[на\ 2\ единицы\ вверх:\]

\[y = - x^{2} + 2\ \ и\ \ y = 0.\]

\[Пересечения\ с\ осью\ x:\]

\[- x^{2} + 2 > 0\]

\[x^{2} < 2\]

\[- \sqrt{2} < x < \sqrt{2}.\]

\[S = \int_{- \sqrt{2}}^{\sqrt{2}}{\left( - x^{2} + 2 \right)\text{\ dx}} =\]

\[= \left. \ \left( - \frac{x^{3}}{3} + 2x \right) \right|_{- \sqrt{2}}^{\sqrt{2}} =\]

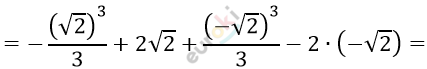
\[= - \frac{2\sqrt{2}}{3} + 2\sqrt{2} - \frac{2\sqrt{2}}{3} + 2\sqrt{2} =\]

\[= 4\sqrt{2} - \frac{4\sqrt{2}}{3} = \frac{12\sqrt{2} - 4\sqrt{2}}{3} =\]

\[= \frac{8\sqrt{2}}{3}.\]

\[Ответ:\ \ \frac{8\sqrt{2}}{3}.\]

\[3)\ y = 1 - x^{2}\text{\ \ }и\ \ y = x^{2} - 1\]

\[1 - x^{2} = x^{2} - 1\]

\[x^{2} + x^{2} = 1 + 1\]

\[2x^{2} = 2\]

\[x^{2} = 1\]

\[x = \pm 1.\]

\[S = \int_{- 1}^{1}{\left( \left( 2 - x^{2} \right) - x^{2} \right)\text{\ dx}} =\]

\[= \left. \ \left( 2 \bullet \frac{x^{1}}{1} - \frac{x^{3}}{3} - \frac{x^{3}}{3} \right) \right|_{- 1}^{1} =\]

\[= \left. \ \left( 2x - \frac{2x^{3}}{3} \right) \right|_{- 1}^{1} =\]

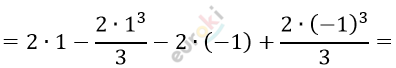
\[2 - \frac{2}{3} + 2 - \frac{2}{3} = 4 - \frac{4}{3} = 2\frac{2}{3}.\]

\[Ответ:\ \ 2\frac{2}{3}.\]

\[4)\ y = x^{3},\ \ \ y = 1,\ \ \ x = - 2;\]

\[x^{3} = 1\ \]

\[x = 1.\]

\[S = \int_{- 2}^{1}{\left( 1 - x^{3} \right)\text{\ dx}} =\]

\[= \left. \ \left( x - \frac{x^{4}}{4} \right) \right|_{- 2}^{1} =\]

\[= 1 - \frac{1^{4}}{4} - ( - 2) + \frac{( - 2)^{4}}{4} =\]

\[= 1 - \frac{1}{4} + 2 + \frac{16}{4} = 3 - \frac{1}{4} + 4 =\]

\[= 7 - \frac{1}{4} = 6\frac{3}{4}.\]

\[Ответ:\ \ 6\frac{3}{4}.\]