Решебник по алгебре и начала математического анализа 10 класс Алимов Задание 976

\[\boxed{\mathbf{976}\mathbf{.}}\]

\[\text{a\ }и\ b - длины\ сторон\ \]

\[прямоугольника:\]

\[b = 2 \bullet \sqrt{R^{2} - a^{2}};\]

\[S(a) = a \bullet b = 2a \bullet \sqrt{R^{2} - a^{2}}.\]

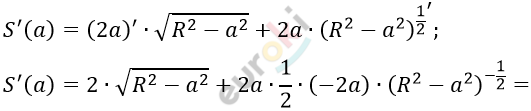
\[= 2\sqrt{R^{2} - a^{2}} - \frac{2a^{2}}{\sqrt{R^{2} - a^{2}}} =\]

\[= 2 \bullet \frac{R^{2} - a^{2} - a^{2}}{\sqrt{R^{2} - a^{2}}} =\]

\[= 2 \bullet \frac{R^{2} - 2a^{2}}{\sqrt{R^{2} - a^{2}}}.\]

\[Промежуток\ возрастания:\]

\[R^{2} - 2a^{2} > 0\]

\[2a^{2} < R^{2}\]

\[a^{2} < \frac{R^{2}}{2}\]

\[- \frac{R}{\sqrt{2}} < a < \frac{R}{\sqrt{2}}.\]

\[a = \frac{R}{\sqrt{2}} - точка\ максимума;\]

\[S\left( \frac{R}{\sqrt{2}} \right) = \frac{2R}{\sqrt{2}} \bullet \sqrt{R^{2} - \frac{R^{2}}{2}} =\]

\[= \frac{2R}{\sqrt{2}} \bullet \sqrt{\frac{R^{2}}{2}} = \frac{2R}{\sqrt{2}} \bullet \frac{R}{\sqrt{2}} = R^{2}.\]

\[Ответ:\ \ R^{2}.\]