Решебник по алгебре и начала математического анализа 10 класс Алимов Задание 1588

\[\boxed{\mathbf{1588}\mathbf{.}}\]

\[f(x) = - \frac{12}{x};\ \ A(3;\ - 4):\]

\[f(3) = - \frac{12}{3} = - 4.\]

\[Касательная\ в\ точке\ A:\]

\[f^{'}(x) = - 12 \bullet \left( \frac{1}{x} \right)^{'} =\]

\[= - 12 \bullet \left( - \frac{1}{x^{2}} \right) = \frac{12}{x^{2}};\]

\[f^{'}(3) = \frac{12}{3^{2}} = \frac{4}{3};\]

\[y = - 4 + \frac{4}{3}(x - 3) =\]

\[= - 4 + \frac{4}{3}x - 4 = \frac{4}{3}x - 8.\]

\[Уравнение\ окружности:\]

\[x^{2} + (y - r)^{2} = r^{2}\]

\[x^{2} + y^{2} - 2yr + r^{2} - r^{2} = 0\]

\[x^{2} + y^{2} - 2yr = 0.\]

\[Окружность\ касается\ прямой\ l:\]

\[x^{2} + \left( \frac{4}{3}x - 8 \right)^{2} - 2r\left( \frac{4}{3}x - 8 \right) = 0\]

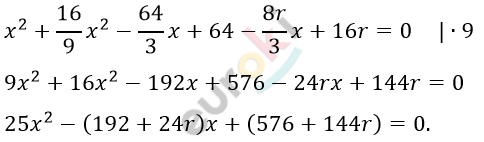
\[= 576r^{2} - 5184r - 20\ 736 =\]

\[= 64\left( 9r^{2} - 81r - 324 \right).\]

\[Одно\ решение\ при\ D = 0:\]

\[9r^{2} - 81r - 324 = 0\]

\[D = 6561 + 11\ 664 = 18\ 225\]

\[r_{1} = \frac{81 - 135}{2 \bullet 9} = - \frac{54}{18} = - 3;\]

\[r_{2} = \frac{81 + 135}{2 \bullet 9} = \frac{216}{18} = 12.\]

\[Ответ:\ \ r = 3\ или\ r = 12.\]