Решебник по алгебре и начала математического анализа 10 класс Колягин Задание 535

\[\boxed{\mathbf{535}.}\]

\[1)\ \sqrt[3]{\sqrt{x - 1} + 2}\]

\[x - 1 \geq 0\]

\[x \geq 1.\]

\[Ответ:при\ x \geq 1.\]

\[2)\ \sqrt[4]{(1 - x)^{2} - 2}\]

\[(1 - x)^{2} - 2 \geq 0\]

\[1 - 2x + x^{2} - 2 \geq 0\]

\[x^{2} - 2x - 1 \geq 0\]

\[D_{1} = 1 + 1 = 2\]

\[x = 1 \pm \sqrt{2}.\]

\[\left( 1 - \sqrt{2} \right)\left( 1 + \sqrt{2} \right) \geq 0\]

\[Ответ:при\ x \leq 1 - \sqrt{2};\ \]

\[\ x \geq 1 + \sqrt{2}.\]

\[3)\ \left( (1 + x)^{- 1} - 3 \right)^{\frac{1}{3}} =\]

\[= \sqrt[3]{\frac{1}{1 + x} - 3}\]

\[1 + x \neq 0\]

\[x \neq - 1.\]

\[Ответ:при\ x \neq - 1.\]

\[4)\ \left( x + 4 \cdot (x - 1)^{- 2} \right)^{- \frac{2}{5}} =\]

\[= \sqrt[5]{\left( \frac{1}{x + \frac{4}{(x - 1)^{2}}} \right)^{2}}\]

\[x + \frac{4}{(x - 1)^{2}} > 0\]

\[\frac{x(x - 1)^{2} + 4}{(x - 1)^{2}} > 0\]

\[\frac{x^{3} - 2x^{2} + x + 4}{(x - 1)^{2}} > 0\]

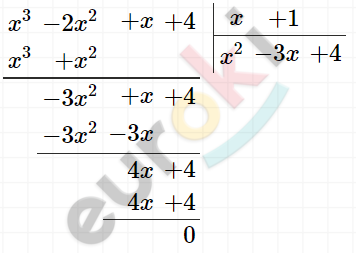
\[x^{2} - 3x + 4 = 0\]

\[D = 9 - 16 = - 7 < 0\]

\[нет\ корней.\]

\[(x - 1)^{2} > 0;\]

\[x + 1 > 0\]

\[x > - 1.\]

\[Ответ:x > - 1.\]