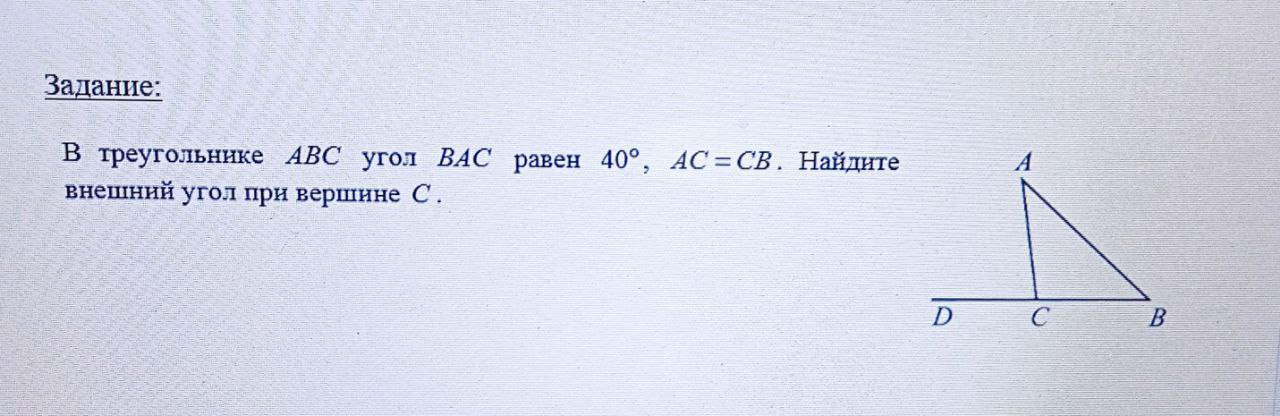
Вопрос:
Задание: В треугольнике ABC угол BAC равен 40°, AC = CB. Найдите внешний угол при вершине C.
Ответ:
Здравствуйте, ребята! Давайте решим эту задачу вместе.
**1. Анализ условия:**
* У нас есть треугольник ABC.
* Угол BAC равен 40° ($\angle BAC = 40^{\circ}$).
* Стороны AC и CB равны (AC = CB), значит треугольник ABC - равнобедренный с основанием AB.
* Нам нужно найти внешний угол при вершине C.
**2. Свойства равнобедренного треугольника:**
В равнобедренном треугольнике углы при основании равны. Следовательно, угол ABC равен углу BAC ($\angle ABC = \angle BAC$). Так как $\angle BAC = 40^{\circ}$, то $\angle ABC = 40^{\circ}$.
**3. Сумма углов треугольника:**
Сумма углов любого треугольника равна 180°. Значит, $\angle BAC + \angle ABC + \angle ACB = 180^{\circ}$.
Подставим известные значения: $40^{\circ} + 40^{\circ} + \angle ACB = 180^{\circ}$.
Отсюда: $\angle ACB = 180^{\circ} - 40^{\circ} - 40^{\circ} = 100^{\circ}$.
**4. Внешний угол треугольника:**
Внешний угол треугольника равен сумме двух других углов, не смежных с ним. Внешний угол при вершине C смежен с углом ACB. Следовательно, сумма внешнего угла при вершине C и угла ACB равна 180° (так как они смежные).
Пусть внешний угол при вершине С равен $\alpha$. Тогда $\alpha + \angle ACB = 180^{\circ}$.
Отсюда $\alpha = 180^{\circ} - \angle ACB = 180^{\circ} - 100^{\circ} = 80^{\circ}$.
**Ответ:** Внешний угол при вершине C равен 80°.
**Развёрнутый ответ для школьника:**
Представь себе треугольник ABC. Угол A (BAC) равен 40 градусам. Так как стороны AC и BC одинаковые, это значит, что углы при основании (углы A и B) тоже одинаковые. Значит, угол B (ABC) тоже равен 40 градусам. Теперь, чтобы найти угол C (ACB), нужно из 180 градусов (это сумма всех углов в треугольнике) вычесть углы A и B. Получается, угол C равен 100 градусам. Внешний угол при вершине C – это угол, который находится "снаружи" треугольника и примыкает к углу C. Вместе они образуют прямую линию, а значит, их сумма равна 180 градусам. Чтобы найти внешний угол, нужно из 180 градусов вычесть угол C (100 градусов). Получается 80 градусов. Вот и всё! Надеюсь, теперь тебе всё понятно.