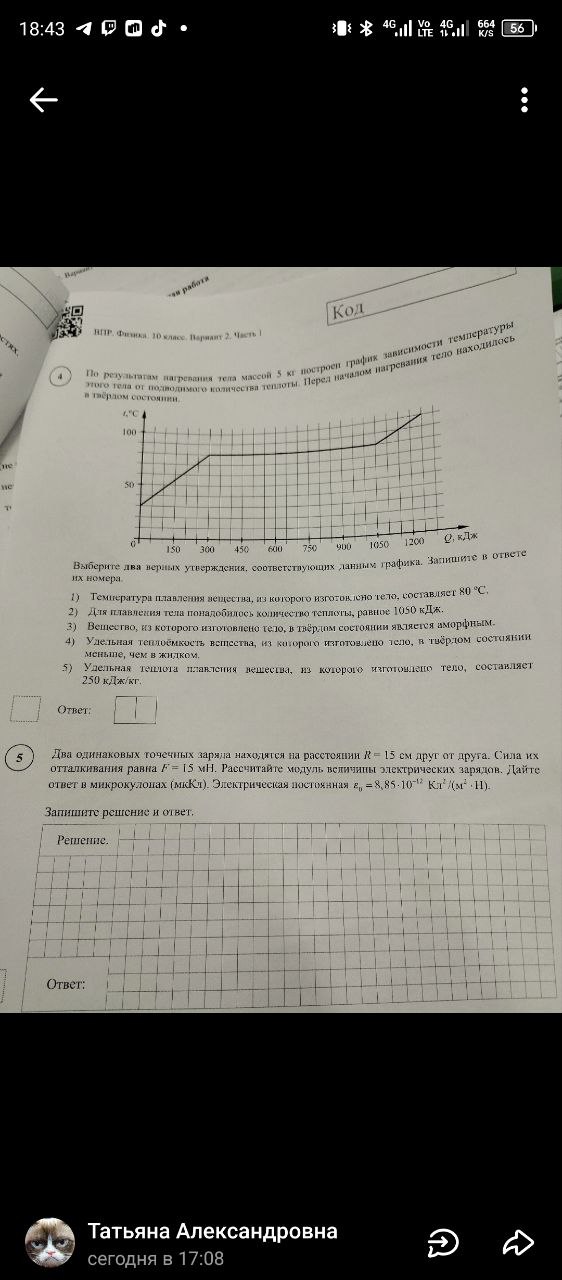
Задание 5: Два одинаковых точечных заряда находятся на расстоянии R = 15 см друг от друга. Сила их отталкивания равна F = 15 мН. Рассчитайте модуль величины электрических зарядов. Дайте ответ в микрокулонах (мкКл). Электрическая постоянная \(ε_0 = 8,85 \cdot 10^{-12} \frac{Кл^2}{м^2 \cdot Н}\).

Решение: Закон Кулона: \(F = k \frac{|q_1 q_2|}{R^2}\), где \(k = \frac{1}{4πε_0}\) Так как заряды одинаковые, \(|q_1| = |q_2| = q\). Тогда \(F = k \frac{q^2}{R^2}\), откуда \(q = \sqrt{\frac{F R^2}{k}} = \sqrt{4πε_0 F R^2}\) Подставим значения: \(R = 15 \) см = 0,15 м \(F = 15 \) мН = 0,015 Н \(ε_0 = 8,85 \cdot 10^{-12} \frac{Кл^2}{м^2 \cdot Н}\) \(q = \sqrt{4π \cdot 8,85 \cdot 10^{-12} \cdot 0,015 \cdot (0,15)^2} = \sqrt{4π \cdot 8,85 \cdot 10^{-12} \cdot 0,015 \cdot 0,0225} \approx \sqrt{3,75 \cdot 10^{-14}} \approx 1,94 \cdot 10^{-7} \) Кл Переведём в микрокулоны: \(1,94 \cdot 10^{-7} \) Кл = 0,194 мкКл Округлим до целого числа: 0,194 мкКл ≈ 0,2 мкКл Ответ: 0,2