Является ли арифметической прогрессией последовательность (an), заданная формулой n–го члена: an=3n^2-2. В случае утвердительного ответа укажите первый член и разность прогрессии.

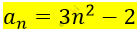
\[a_{n + 1} = 3 \cdot (n + 1)^{2} - 2 =\]

\[= 3n^{2} + 6n + 3 - 2 =\]

\[= 3n^{2} + 6n + 1\]

\[a_{n + 1} - a_{n} =\]

\[= 3n^{2} + 6n + 1 - 3n^{2} + 2 =\]

\[= 6n + 3 \Longrightarrow не\ является.\ \]