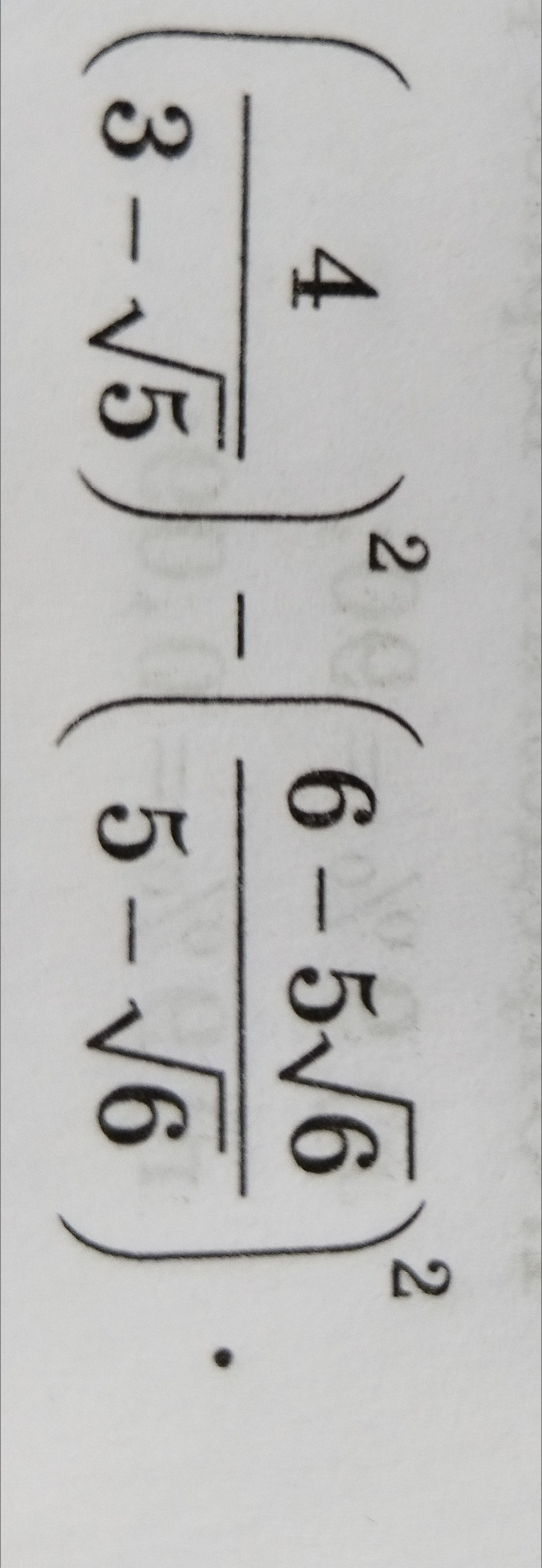
Вычислите:$\left(\frac{4}{3-\sqrt{5}}\right)^2 - \left(\frac{6-5\sqrt{6}}{5-\sqrt{6}}\right)^2$

Здравствуйте, ученики! Сегодня мы разберем решение следующего примера: $\left(\frac{4}{3-\sqrt{5}}\right)^2 - \left(\frac{6-5\sqrt{6}}{5-\sqrt{6}}\right)^2$ Для начала упростим каждое из выражений в скобках, избавляясь от иррациональности в знаменателе. **Шаг 1: Упростим первое выражение** Умножим числитель и знаменатель дроби $\frac{4}{3-\sqrt{5}}$ на сопряженное выражение к знаменателю, то есть на $3+\sqrt{5}$: $\frac{4}{3-\sqrt{5}} = \frac{4(3+\sqrt{5})}{(3-\sqrt{5})(3+\sqrt{5})}$ Используем формулу разности квадратов: $(a-b)(a+b) = a^2 - b^2$ $\frac{4(3+\sqrt{5})}{3^2 - (\sqrt{5})^2} = \frac{4(3+\sqrt{5})}{9 - 5} = \frac{4(3+\sqrt{5})}{4} = 3+\sqrt{5}$ Теперь возведем полученное выражение в квадрат: $(3+\sqrt{5})^2 = 3^2 + 2 \cdot 3 \cdot \sqrt{5} + (\sqrt{5})^2 = 9 + 6\sqrt{5} + 5 = 14 + 6\sqrt{5}$ **Шаг 2: Упростим второе выражение** Умножим числитель и знаменатель дроби $\frac{6-5\sqrt{6}}{5-\sqrt{6}}$ на сопряженное выражение к знаменателю, то есть на $5+\sqrt{6}$: $\frac{6-5\sqrt{6}}{5-\sqrt{6}} = \frac{(6-5\sqrt{6})(5+\sqrt{6})}{(5-\sqrt{6})(5+\sqrt{6})}$ $\frac{30 + 6\sqrt{6} - 25\sqrt{6} - 5 \cdot 6}{25 - 6} = \frac{30 - 19\sqrt{6} - 30}{19} = \frac{-19\sqrt{6}}{19} = -\sqrt{6}$ Теперь возведем полученное выражение в квадрат: $(-\sqrt{6})^2 = 6$ **Шаг 3: Вычислим разность** Теперь вычтем результаты: $(14 + 6\sqrt{5}) - 6 = 8 + 6\sqrt{5}$ **Ответ:** $\bf{8 + 6\sqrt{5}}$ **Развернутый ответ для школьника:** Итак, у нас было сложное выражение с дробями и корнями. Чтобы его упростить, мы сначала избавились от корней в знаменателе каждой дроби. Для этого мы умножили числитель и знаменатель каждой дроби на специальное выражение, которое называется сопряженным к знаменателю. Затем мы возвели полученные результаты в квадрат и вычли их. В итоге получили простой ответ: $8 + 6\sqrt{5}$. Надеюсь, теперь все понятно!