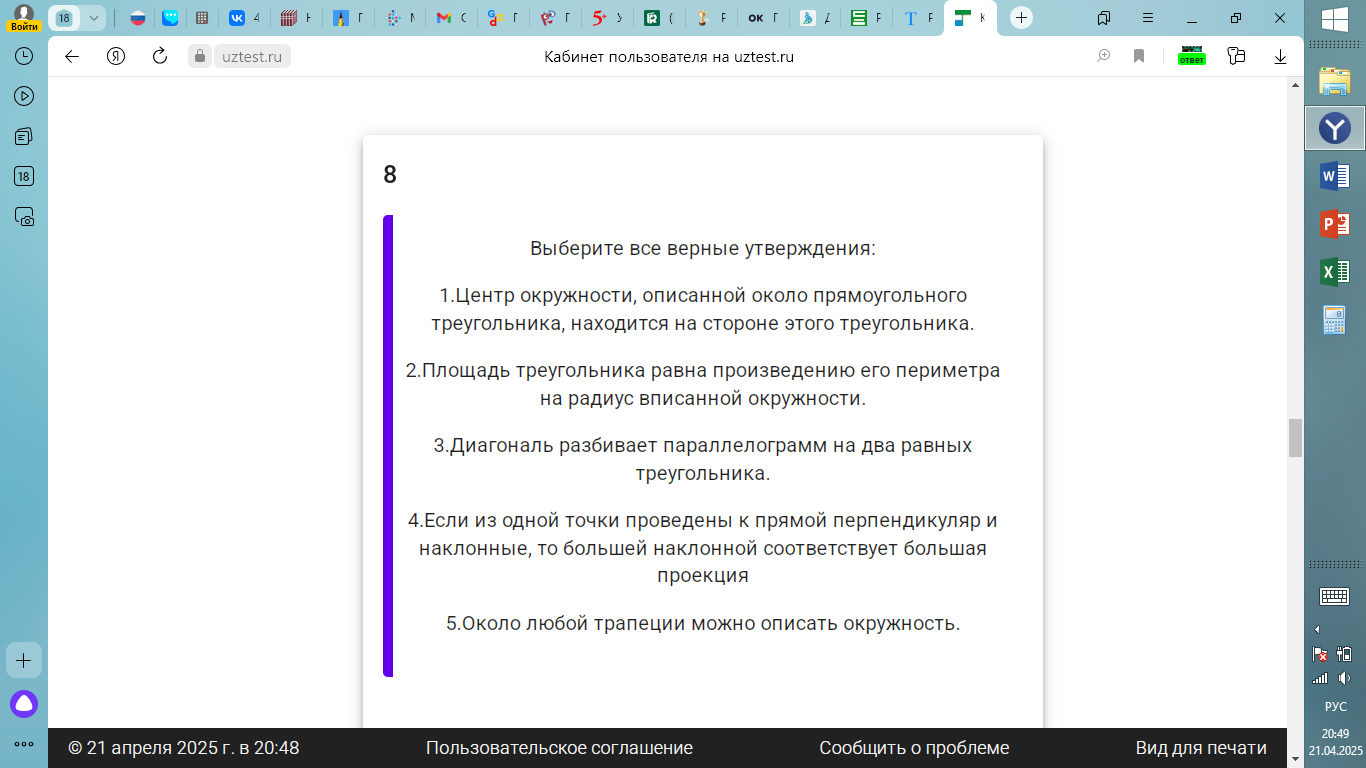
Выберите все верные утверждения: 1. Центр окружности, описанной около прямоугольного треугольника, находится на стороне этого треугольника. 2. Площадь треугольника равна произведению его периметра на радиус вписанной окружности. 3. Диагональ разбивает параллелограмм на два равных треугольника. 4. Если из одной точки проведены к прямой перпендикуляр и наклонные, то большей наклонной соответствует большая проекция 5. Около любой трапеции можно описать окружность.

Разберем каждое утверждение: 1. Центр окружности, описанной около прямоугольного треугольника, находится на середине гипотенузы, которая является стороной треугольника. Это утверждение верно. 2. Площадь треугольника не равна произведению его периметра на радиус вписанной окружности. Площадь треугольника равна половине произведения периметра на радиус вписанной окружности: (S = rac{1}{2}Pr), где (S) - площадь, (P) - периметр, (r) - радиус вписанной окружности. Это утверждение неверно. 3. Диагональ разбивает параллелограмм на два равных треугольника. Это утверждение верно. 4. Если из одной точки проведены к прямой перпендикуляр и наклонные, то большей наклонной соответствует большая проекция. Это утверждение верно. 5. Около трапеции можно описать окружность только тогда, когда она равнобедренная. Поэтому, утверждение "Около любой трапеции можно описать окружность" - неверно. Ответ: Верные утверждения: 1, 3, 4.