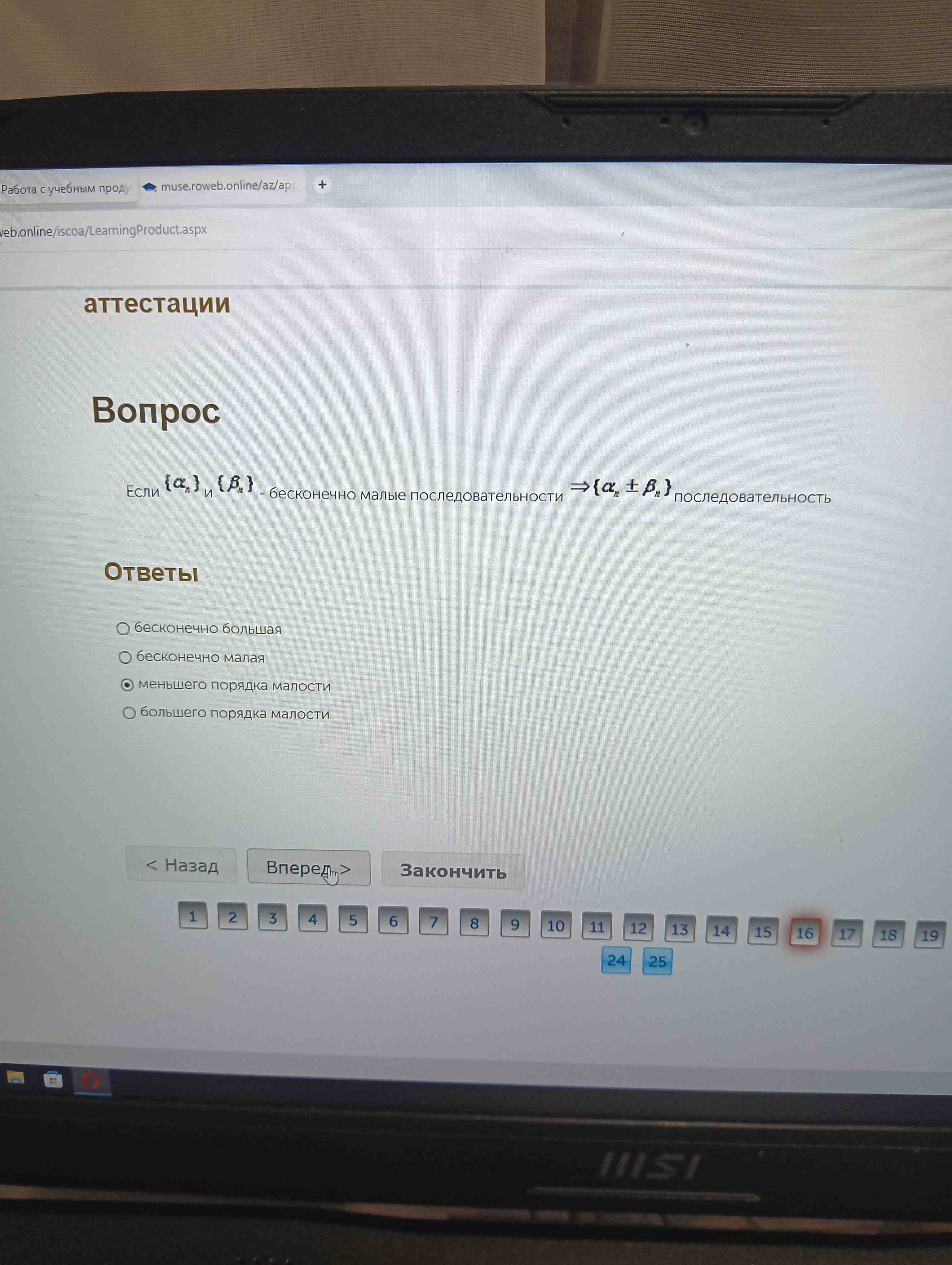
Вопрос из теста: Если $\alpha_n$ и $\beta_n$ - бесконечно малые последовательности, то какой последовательностью будет их сумма или разность $\alpha_n \pm \beta_n$?

Давайте разберемся с этим вопросом. Условие задачи говорит о том, что у нас есть две бесконечно малые последовательности: $\alpha_n$ и $\beta_n$. Бесконечно малая последовательность – это последовательность, предел которой равен нулю, то есть $\lim_{n \to \infty} \alpha_n = 0$ и $\lim_{n \to \infty} \beta_n = 0$. Нам нужно определить, что будет с последовательностью, полученной в результате сложения или вычитания этих двух бесконечно малых последовательностей ($\alpha_n \pm \beta_n$). Воспользуемся свойствами пределов. Предел суммы (или разности) двух последовательностей равен сумме (или разности) их пределов, если эти пределы существуют: $$\lim_{n \to \infty} (\alpha_n \pm \beta_n) = \lim_{n \to \infty} \alpha_n \pm \lim_{n \to \infty} \beta_n = 0 \pm 0 = 0$$ Таким образом, предел последовательности $\alpha_n \pm \beta_n$ равен нулю. Следовательно, эта последовательность тоже является бесконечно малой. **Ответ:** Если $\alpha_n$ и $\beta_n$ – бесконечно малые последовательности, то их сумма или разность $\alpha_n \pm \beta_n$ также является **бесконечно малой** последовательностью.