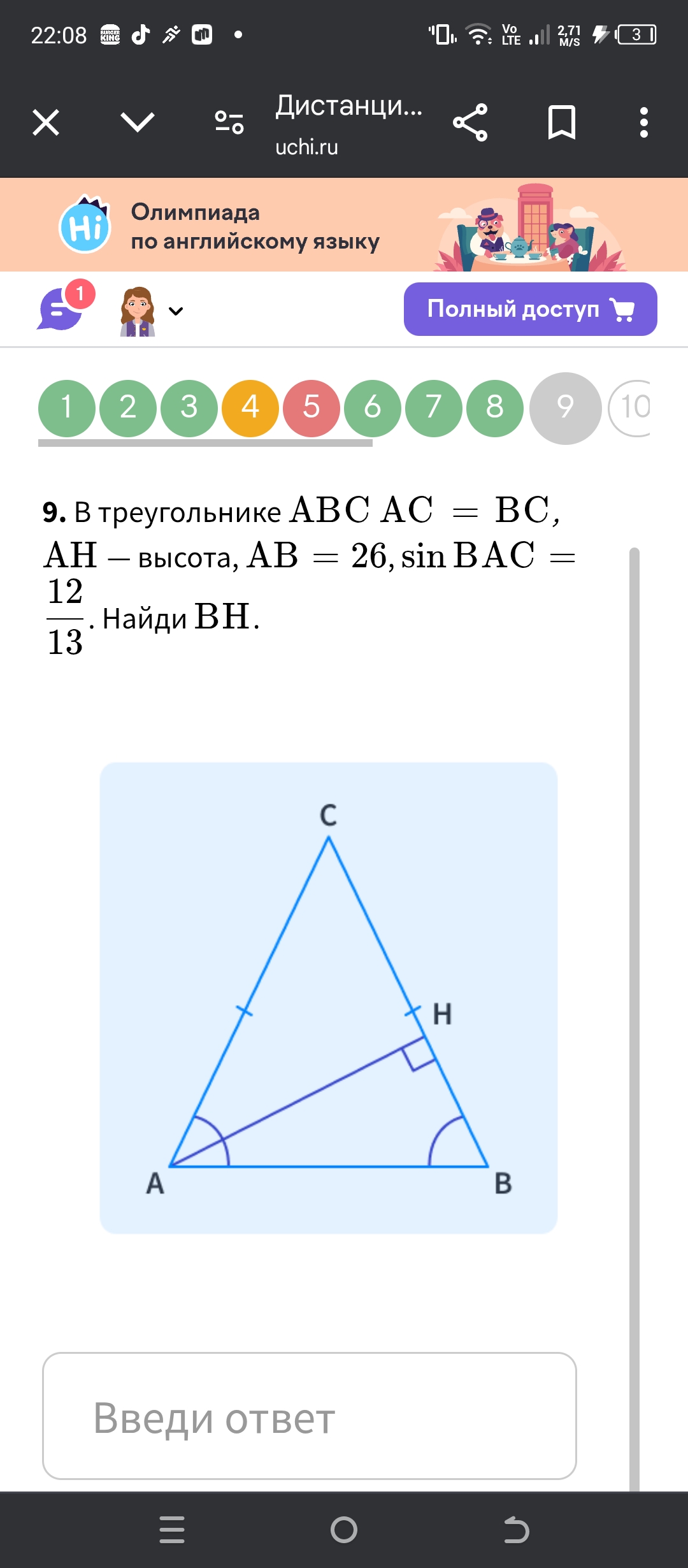
9. В треугольнике ABC AC = BC, AH - высота, AB = 26, sin BAC = \frac{12}{13}. Найди BH.

Поскольку в треугольнике ABC AC = BC, то треугольник ABC является равнобедренным. Угол BAC равен углу ABC. Известно, что \(\sin BAC = \frac{12}{13}\). Наша задача - найти BH. 1. **Найдем cos BAC:** Мы знаем, что \(\sin^2 \alpha + \cos^2 \alpha = 1\). Следовательно: \(\cos^2 BAC = 1 - \sin^2 BAC = 1 - \left(\frac{12}{13}\right)^2 = 1 - \frac{144}{169} = \frac{169 - 144}{169} = \frac{25}{169}\) Таким образом, \(\cos BAC = \sqrt{\frac{25}{169}} = \frac{5}{13}\) (так как угол BAC острый, косинус положительный). 2. **Рассмотрим треугольник ABH:** AH - высота, следовательно, треугольник ABH прямоугольный. В этом треугольнике: \(\cos BAC = \frac{AH}{AB}\) У нас есть AB = 26 и \(\cos BAC = \frac{5}{13}\). Поэтому: \(\frac{BH}{AB} = \cos ABC = \cos BAC = \frac{5}{13}\) 3. **Выразим BH:** \(BH = AB \cdot \cos ABC = 26 \cdot \frac{5}{13} = 2 \cdot 5 = 10\) Таким образом, BH = 10. **Ответ:** BH = **10**