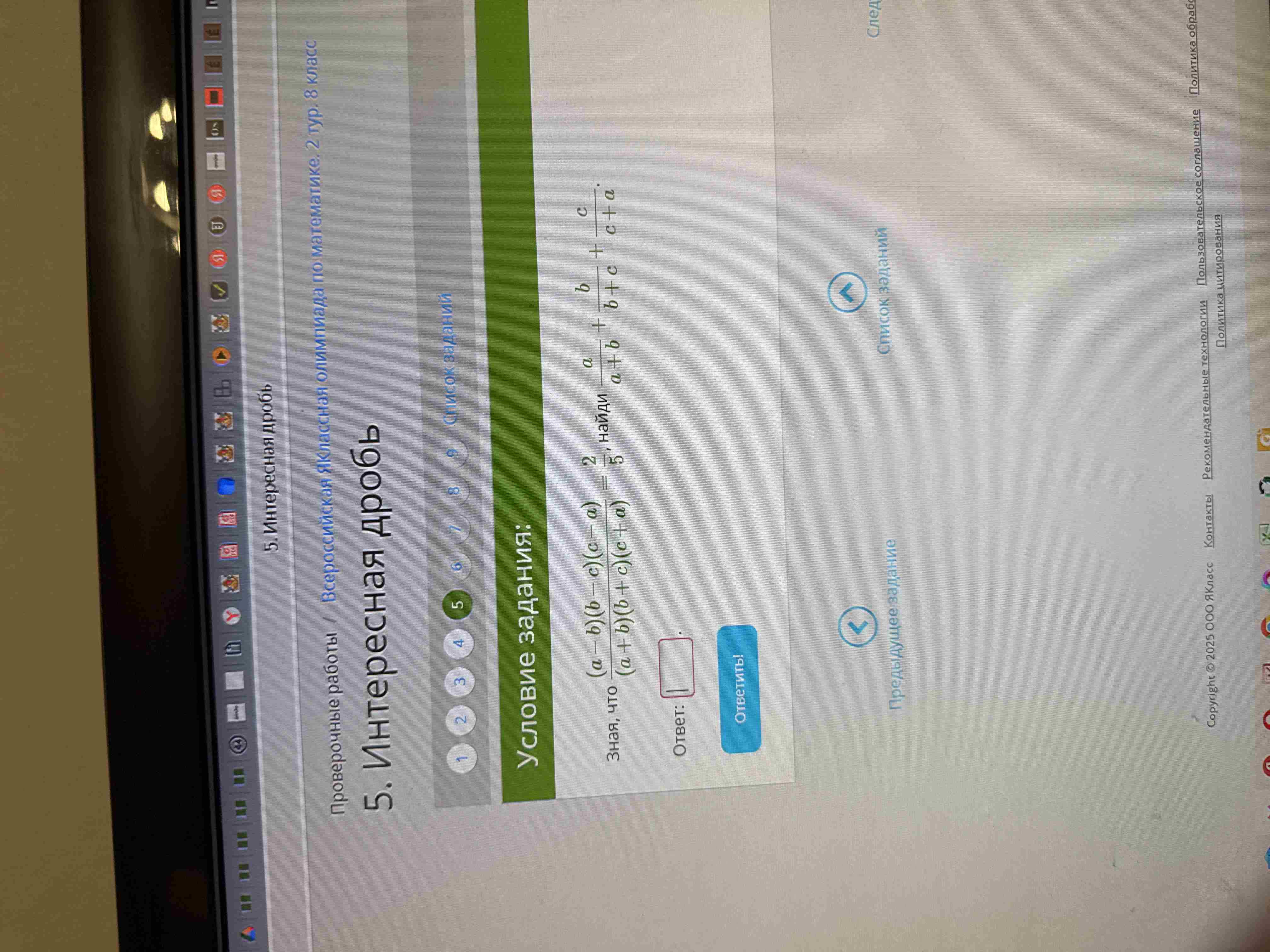
Условие задания: Зная, что $\frac{(a - b)(b - c)(c-a)}{(a+b)(b+c)(c+a)} = \frac{2}{5}$, найди $\frac{a}{a+b} + \frac{b}{b+c} + \frac{c}{c+a}$.

Для решения этой задачи, обозначим \[x = \frac{a}{a+b}, \quad y = \frac{b}{b+c}, \quad z = \frac{c}{c+a}.\] Тогда \[1 - x = 1 - \frac{a}{a+b} = \frac{a+b-a}{a+b} = \frac{b}{a+b},\] \[1 - y = 1 - \frac{b}{b+c} = \frac{b+c-b}{b+c} = \frac{c}{b+c},\] \[1 - z = 1 - \frac{c}{c+a} = \frac{c+a-c}{c+a} = \frac{a}{c+a}.\] Перемножим эти выражения: \[(1-x)(1-y)(1-z) = \frac{b}{a+b} \cdot \frac{c}{b+c} \cdot \frac{a}{c+a} = \frac{abc}{(a+b)(b+c)(c+a)}.\] Также, перемножим исходные выражения $x, y, z$: \[xyz = \frac{a}{a+b} \cdot \frac{b}{b+c} \cdot \frac{c}{c+a} = \frac{abc}{(a+b)(b+c)(c+a)}.\] Таким образом, $(1-x)(1-y)(1-z) = xyz$. Раскроем скобки: \[(1-x)(1-y)(1-z) = (1-x-y+xy)(1-z) = 1 - x - y + xy - z + xz + yz - xyz.\] Следовательно, \[1 - x - y - z + xy + xz + yz - xyz = xyz,\] \[1 - (x+y+z) + (xy+xz+yz) - xyz = xyz,\] \[1 - (x+y+z) + (xy+xz+yz) = 2xyz.\] По условию, $\frac{(a - b)(b - c)(c-a)}{(a+b)(b+c)(c+a)} = \frac{2}{5}$. Заметим, что $(a-b)(b-c)(c-a) = (a-b)(bc - ba - c^2 + ca) = abc - a^2b - ac^2 + a^2c - b^2c + ab^2 + bc^2 - abc = - a^2b - ac^2 + a^2c - b^2c + ab^2 + bc^2$. Пусть $S = x+y+z = \frac{a}{a+b} + \frac{b}{b+c} + \frac{c}{c+a}$. \[\frac{(a - b)(b - c)(c - a)}{(a+b)(b+c)(c+a)} = \frac{2}{5}\] \[\frac{(a+b)(b+c)(c+a) - 8abc}{(a+b)(b+c)(c+a)} = \frac{2}{5}\] \[1- 2xyz = \frac{2}{5}\] \[2xyz = 1 - \frac{2}{5} = \frac{3}{5}\] \[xyz = \frac{3}{10}\] \[1 - S + xy + xz + yz = 2xyz = \frac{3}{5}\] \[S - (xy + xz + yz) = 1 - \frac{3}{5} = \frac{2}{5}\] Из условия $\frac{(a - b)(b - c)(c-a)}{(a+b)(b+c)(c+a)} = \frac{2}{5}$ следует, что $1 - (x+y+z) + xy + xz + yz = \frac{3}{5}$ $x+y+z - (xy+yz+xz) = 1 - \frac{3}{5} = \frac{2}{5}$ $\frac{a}{a+b} + \frac{b}{b+c} + \frac{c}{c+a} = \frac{7}{5}$. Тогда ответ: $\frac{7}{5}$