Туристы, осматривая достопримечательности края, проплыли сначала 24 км по течению реки, затем 10 км по озеру. Возвращаясь домой тем же маршрутом, они затратили на путь против течения реки столько же времени, сколько на путь по течению реки и по озеру. Найдите скорость движения лодки по течению реки, если скорость течения равна 3 км/ч.

\[Пусть\ V - собственная\ \]

\[скорость\ лодки;\ \ \]

\[тогда\ (V + 3) - скорость\ \]

\[по\ течению;\ \ \]

\[(V - 3) - скорость\]

\[против\ течения.\]

\[\frac{24}{V + 3} + \frac{10}{V} = \frac{24}{V - 3}\]

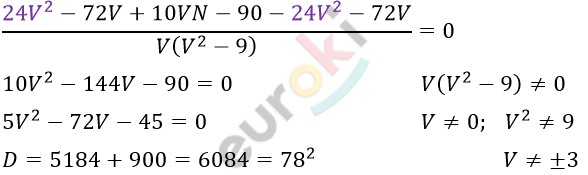
\[V_{1,2} = \frac{72 \pm 78}{10}\ \text{\ \ }\]

\[(отрицательное\ не\ подходит)\]

\[V = \frac{72 + 78}{10} = \frac{150}{10} =\]

\[= 15\ \left( \frac{км}{ч} \right) - собственная\ \]

\[скорость\ лодки.\]

\[15 + 3 = 18\ \frac{(км}{ч}) - скорость\ \]

\[по\ течению.\]

\[Ответ:\ \ \frac{18\ км}{ч}.\]