При каком отрицательном значении параметра p один из корней квадратного уравнения x^2+px+36=0 на 4 меньше другого?

\[x^{2} + px + 36 = 0\]

\[D = p^{2} - 4 \cdot 36 = p^{2} - 144 > 0\]

\[так\ как\ уравнение\ \]

\[имеет\ 2\ корня.\]

\[x_{1,2} = \frac{- p \pm \sqrt{p² - 144}}{2}\]

\[Так\ как\ x_{1} - x_{2} = 4;\ \ \ то:\]

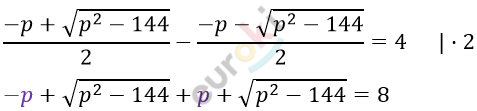
\[2\sqrt{p^{2} - 144} = 8\]

\[\sqrt{p^{2} - 144} = 4\]

\[p^{2} - 144 = 16\]

\[p^{2} = 160\]

\[p = \pm \sqrt{160}\]

\[Так\ как\ p < 0;\ \ то\ \ p = - 4\sqrt{10}.\]

\[Ответ:при\ \ p = - 4\sqrt{10}.\]