Сумма седьмого и девятого членов арифметической прогрессии равна 12, а произведение шестого и десятого членов равно -28. Найдите разность и первый член данной прогрессии.

\[\left\{ \begin{matrix}
a_{7} + a_{9} = 12\ \ \\
a_{6} \cdot a_{10} = - 28 \\
\end{matrix}\text{\ \ } \right.\ \]

\[a_{7} = a_{1} + 6d\ \ \ \]

\[\ a_{9} = a_{1} + 8d\]

\[a_{6} = a_{1} + 5d\ \ \ \ \]

\[a_{10} = a_{1} + 9d\]

\[\left\{ \begin{matrix}
a_{1} + 6d + a_{1} + 8d = 12\ \ \ \ \\
\left( a_{1} + 5d \right)\left( a_{1} + 9d \right) = - 28 \\
\end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix}
2a_{1} + 14d = 12\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\
a_{1}^{2} + 9a_{1}d + 5a_{1}d + 45d^{2} = - 28 \\
\end{matrix} \right.\ \]

\[\left\{ \begin{matrix}
a_{1} + 7d = 6 \longrightarrow a_{1} = 6 - 7d \\
a_{1}^{2} + 14a_{1}d + 45d^{2} = - 28\ \ \ \\
\end{matrix} \right.\ \]

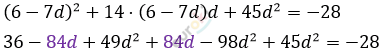
\[- 4d^{2} = - 64\ \ \ \]

\[d^{2} = - 16\ \ \ \ \]

\[d = \pm 4.\]

\[a_{1} = 6 - 7 \cdot ( \pm 4) = 6 \pm 28 =\]

\[= 34;\ \ \ - 22\]

\[Ответ:\ \ \ a_{11} = 34;\ \ \ \ \ d_{1} = - 4\ \ \]

\[\ или\ \ \ \ a_{12} = - 22;\ \ \ \ d_{2} = 4.\]