Сумма пятого и восьмого членов арифметической прогрессии на 15 больше суммы седьмого и десятого. Найдите разность прогрессии.

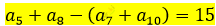
\[a_{5} = a_{1} + 4d\]

\[a_{7} = a_{1} + 6d\]

\(a_{8} = a_{1} + 7d\)

\[a_{10} = a_{1} + 9d\]

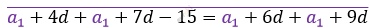
\[11d - 15 = 15d\]

\[4d = - 15\]

\[d = - \frac{15}{4} = - 3,75.\]

\[Ответ:d = - 3,75.\]