Случайным образом выбирают одно из решений неравенства |x-2|<5. Какова вероятность того, что оно окажется и решением неравенства x^2-16>0?

\[|x - 2| < 5\]

\[\left\{ \begin{matrix}
x - 2 \geq 0 \\
x \geq 2\ \ \ \ \ \ \ \ \\
x - 2 < 5 \\
x < 7\ \ \ \ \ \ \ \\
\end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ }\text{\ \ \ \ }\left\{ \begin{matrix}
x - 2 < 0\ \ \ \\
x < 2\ \ \ \ \ \ \ \ \ \ \ \\
x - 2 > - 5 \\
x > - 3\ \ \ \ \ \ \ \ \\
\end{matrix} \right.\ \]

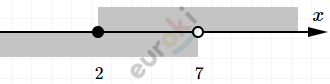
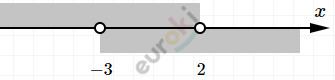
\[Совместим\ - 3 < x < 7;\ \ \]

\[то\ есть\ всего\ 10\ ответов.\]

\[x^{2} - 16 > 0\]

\[(x - 4)(x + 4) > 0\]

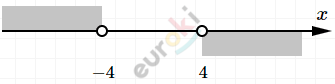
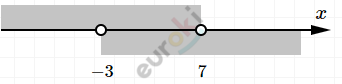
\[То\ есть\ совместный\ ответ\]

\[\ (4;7).\]

\[Р = \frac{2}{10} = 0,2.\]

\[Ответ:0,2.\]